下圖左是藝術家杜勒(Albrecht Dürer)的版畫《憂鬱》。


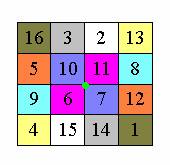
注意到了嗎?在圖的右上角有一個四階魔方陣,見上圖右,這個魔方陣是由杜勒自己發現的。他創作這幅版畫的時候正值文藝復興時期,當時的占星家認為四階魔方陣可以驅除憂鬱,所以他就將這個魔方陣放入作品之中。而且,這個魔方陣還有一個很妙的地方,它的底邊15, 14正是這幅作品完成的年代1514年。

注意到上面的4階魔方陣和之前的3階魔方陣擁有的另一個共同性質:任兩個對稱於中心點的位置上的數字其和都是n2 + 1 ――這樣的魔方陣我們稱之為對稱魔方陣。
如下圖,上面的4階魔方陣對稱於中心點的位置上的數字其和都是42 + 1 = 17。
現在我們已經很了解3階的魔方陣是怎麼一回事了,而且也看過一個四階魔方陣的例子,於是我們很自然會想知道:是否對於任意正整數n都存在一個n階的魔方陣?
如果n > 3呢?對於這個問題,大約30年前德國數學家L. Bieberbach證明了:
「對於任意大於等於3的數n,都存在一個n階的魔方陣。」
是不是數字愈多就可以組合出愈多種的魔方陣(同構的魔方陣視同一種)?
n = 3
有唯一一個魔方陣。
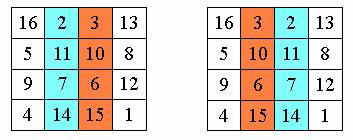
n = 4
下面是兩個不同構的4階魔方陣
似乎n愈大,不同構的n階魔方陣就愈多。到底n階的魔方陣有幾個?
n = 3:1個
n = 4:880個
n = 5:275305224個(靠計算機的幫忙)
你有沒有什麼好的方法可以計算魔方陣的個數呢?