Suppose that
![]() and
and
![]() are both given as functions of a third variable
are both given as functions of a third variable
![]() (called
parameter
) by the equations
(called
parameter
) by the equations
![]()
![]()
(called
parametric equations
). Each value of
![]() determines a point (
determines a point (
![]() ), which we can plot in a coordinate plane. As
), which we can plot in a coordinate plane. As
![]() varies, the point (
varies, the point (
![]() ) = (
) = (
![]() ) varies and traces out a curve
C
, which is called a
parametric curve
. If
) varies and traces out a curve
C
, which is called a
parametric curve
. If
![]() and
and
![]() are defined for all
are defined for all
![]() in [
in [
![]() ], then (
f(a), g(a)
) is called the
initial point
of
C
and (
f(b), g(b)
) is called the
final point
of
C
. Imagine that a particle moving along the curve
C
, we can interpret
], then (
f(a), g(a)
) is called the
initial point
of
C
and (
f(b), g(b)
) is called the
final point
of
C
. Imagine that a particle moving along the curve
C
, we can interpret
![]() as time and (
as time and (
![]() ) = (
) = (
![]() ) as the position of the particle at time
) as the position of the particle at time
![]() . We say
C
is
closed
if the initial point and the final point of
C
are the same.
. We say
C
is
closed
if the initial point and the final point of
C
are the same.
Consider the curve with parametric equations
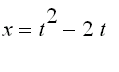
![]()
the graphs below show how the curve moves with the parameter
![]() .
.
>
with(plots):
f := t -> t^2 - 2*t:
g := t -> t + 1:
c := n -> plot( [ t^2 - 2*t, t + 1, t = -0.001..n ], scaling = constrained,
thickness = 2 ):
t := k -> textplot( [ f(k) - 0.34, g(k) + 0.25, `t =` ], 'align = LEFT' ):
tt := n -> display( seq( t(k), k = 0..n ) ):
t1 := k -> textplot( [ f(k) - 0.14, g(k) + 0.25, k ] ):
tt1 := n -> display( seq( t1(k), k = 0..n ) ):
pp := k -> plot( [ [ f(k), g(k) ] ], style = point, symbol = circle, color = blue ):
pp1 := n -> display( seq( pp(k), k = 0..n ) ):
p := n -> display( c(n), tt(n), tt1(n), pp1(n) ):
display( seq( p(n), n = 0..4 ), insequence = true, scaling = constrained );
![[Maple Plot]](lab_parametricCurve_into3_001.jpg)
Notice that the consecutive points marked on the curve appear at equal time intervals but not at equal distances. That is because the particle slows down and speeds up as
![]() increases. Moreover, the curve presented by the parametric equations is part of a parabola
increases. Moreover, the curve presented by the parametric equations is part of a parabola
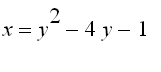 .
.
One of the advantages of parametric description of curves is that they are convenient for "combined motions." This lets us plot curves obtained by adding parametric motions. Here is an example :
The curve traced out by a point
![]() on the circumference of a circle of radius
on the circumference of a circle of radius
![]() as the circle rolls with a constant angular speed
as the circle rolls with a constant angular speed
![]() along a straight line is called
cycloid
. Play the animation below to get a better picture.
along a straight line is called
cycloid
. Play the animation below to get a better picture.
![[Maple Plot]](images/cycloid_ani1.jpg)
![[Maple Plot]](images/GrapicDesign31.gif)
![[Maple Plot]](images/animate_hypocycloid1.jpg)
![[Maple Plot]](images/lab_Hypocycloids_and_Epicycloids_ans4.gif)
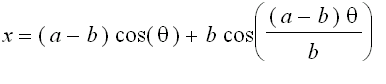
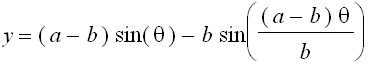
![[Maple OLE 2.0 Object]](images/lab_Hypocycloids_and_Epicycloids_ans10.gif)
![[Maple OLE 2.0 Object]](images/lab_Hypocycloids_and_Epicycloids_ans13.gif) ,
,
![[Maple OLE 2.0 Object]](images/lab_Hypocycloids_and_Epicycloids_ans14.gif)
![[Maple OLE 2.0 Object]](images/lab_Hypocycloids_and_Epicycloids_ans15.gif)
![[Maple OLE 2.0 Object]](images/lab_Hypocycloids_and_Epicycloids_ans16.gif)
![[Maple OLE 2.0 Object]](images/lab_Hypocycloids_and_Epicycloids_ans17.gif)
![[Maple Plot]](images/animate_hypocycloid2.jpg)
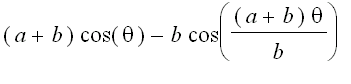
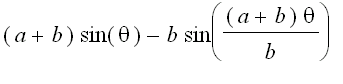 .
.
![[Maple Plot]](images/lab_Hypocycloids_and_Epicycloids_ans234.gif)
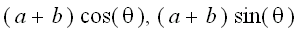 ),
), are radii of the larger circle and the smaller circle, respectively.
are radii of the larger circle and the smaller circle, respectively.
![[Maple OLE 2.0 Object]](images/lab_Hypocycloids_and_Epicycloids_ans240.gif) ,
,
![[Maple OLE 2.0 Object]](images/lab_Hypocycloids_and_Epicycloids_ans242.gif)
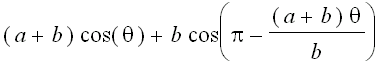 =
=
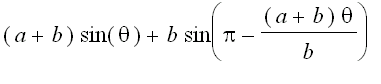 =
=