¡@

Double Integral Over General Regions

Download Maple Worksheet

1. Evaluate , where D  is the region bounded by the parabolas  and .

First, by solving

,

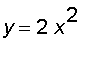
we find the intersections of the parabolas are () and (). Here is the picture if the region D :

 

We see that fix x  in [], y  goes from  to , so we get

=

=  =  

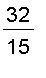
We can view the double integral as the volume of the solid bounded by the planes (colored blue), and the cylinders  (colored yellow),  (colored green).

3DVIEW3DVIEW

2. Find the volume of the solid that lies under the paraboloid and above the region D  in the xy -plane bounded by the line and the parabola .

The solid is bounded by the paraboloid (colored blue), the plane (colored yellow), the cylinders (colored green) and the xy -plane. Here is a picture of the solid :

3DVIEW3DVIEW

By solving

   

 

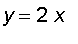
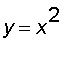
we find the intersections of the parabolas are () and (). Here is the picture if the region D :

 

We see that fix x  in [], y  goes from  to , so we get that the volume equals

  =   

=   =  

¡@

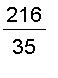
3. Evaluate , where D  is the region bounded by the line  and the parabola .

by solving

   

  ,

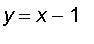
we find the intersections of the parabolas are () and (). Here is the picture if the region D :

 

¡@

We see that fix y  in [], x  goes from  to , so

  =    

=    =

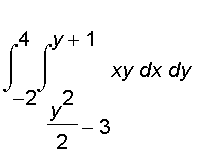
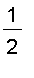
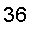
We can view the double integral as the "signed volume" of the solid bounded by the hyperbolic paraboloid    (colored blue), the cylinders  (colored green), and the planes    (colored yellow) and  (colored pink).

3DVIEW

 
3DVIEW

4. Find the volume of the tetrahedron bounded by the planes , , , and .

The vertices of the tetrahedron are (), (), () and  ().

3DVIEW

The volume of the tetrahedron is given by , where D  is the region bounded by the lines  and .

 

We see that fix x  in [ ], y  goes from  to , so we get that the volume equals

=  

=  =    

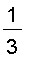
If we integrate  first, we have to split the iterated integral into two parts :

 

 =  

¡@

5. Evaluate the iterated integral .

If we try to evaluate the integral as it stands, then we need to find the antiderivatives of . But this is impossible, because  does not have a closed form. So we must change the order of integration.

Note that

 =

where D  =  {( ) | , }.  

 

From the animation below, we see an alternative description of D is

D  =  {( ) | , }.  

 

Hence, by Fubini's theorem, we have

 =  

=    =   =    .

¡@

¡@

6. Find the volume of the solid bounded by the plane  and the paraboloid .

3DVIEW

The volume equals to , where D  is the unit disk .

In terms of Cartesian coordinates, D is bounded by  and  , so the volume is given by

 =   .

However, the iterated integral is rather complicated to compute. Note that D is rather easy to described using polar coordinates, namely, .

The volume of the solid is

=    =

¡@

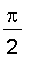
7. Find the volume of the solid that lies under the paraboloid , above the xy -plane, and inside the cylinder .

The solid lies above the disk D  whose boundary circle has equation , i.e., . Its equation in polar coordinates is given by , where  is in [].

 

The volume of the solid is

 =  

=       =    .

¡@

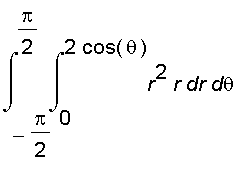
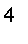
8. Find the volume of the solid that bounded by the paraboloid , the plane , the xy -plane, and inside the cylinder .

 

The volume of the solid can be computed as , where  is the volume of solid bounded by the cylinder ,  and , which is .

while  is the volume of solid shown below.

3DVIEW

By symmetry  is 2 times the volume of the solid that lies above the first quadrant, so

where  R  is the region shown below.

Fix in ,  goes from  to , and f ix  in  ,  goes from  to . So we have

=    =

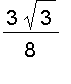
Therefore, the required volume is .

---

Download Maple Worksheet