L ' Hospital's Rule
Suppose that
and
.
Recall that if
, then
.
If
but
, then
.
For the case where both
and
are 0, we are not sure whether the limit
exists or not. In fact, although the limit exists, it is not obvious what is its value. In this case,
is called an indeterminate form of type
.
Let's study the following three easy examples first :
Example 1
,
,
.
![[Maple Plot]](images/suppl_LHospital16.gif)
Example 2
,
,
does not exist.
Example 3
,
,
.
![[Maple Plot]](images/suppl_LHospital23.gif)
Since f and g are differentiable at 0, the graphs of f and g resemble the tangent lines of
and
at (
), respectively. The derivative of
at 0 equals 0 and the derivative of
at 0 equals 1, we can see that the graphs of f and g look very much like the lines
and
. It is not surprised that
.
Suppose now we want to find
, let's plot
and
on the same screen for x near 1.
![[Maple Plot]](images/suppl_LHospital35.gif)
For x near 1, the graphs of
and
both look like the straight line
, it is reasonable to guess that
. The values of
for x near 1 also confirm our guess.
f:=x->ln(x)/(x-1):
for n from 1 to 9
do
x:=1.1-n/100:
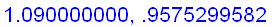
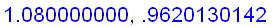
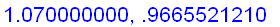
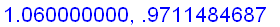
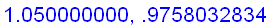
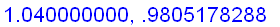
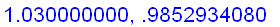
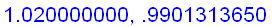
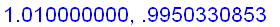
n:='n': x:='x':
for n from 1 to 9
do
x:=0.9+n/100:
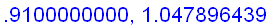
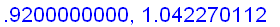
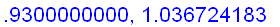
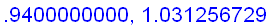
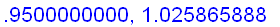
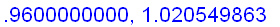
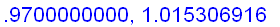
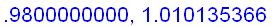
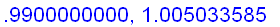
Intuitively, if x is sufficiently close to 1, then the value of
is close to
+ f ' (1) (
) =
Hence,
=
.
Another case where a limit is not obvious is the limit of the form
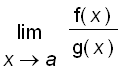
where both
and
equals
or
and it is called an indeterminate form of type
. For instance,
.
![[Maple Plot]](images/suppl_LHospital72.gif)
From the plot above, we see that when x is sufficiently large the graph of
looks like a constant function. Since
,
for a sufficiently large the slope of the tangent line of
at
is almost 0.
We would expect that
.
We can also see this by observing the values of
for x large.
f:=x->ln(x)/(x-1):
for n from 1 to 6
do
x:=10^(n+3):
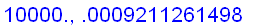
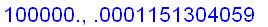
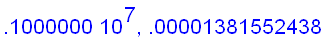
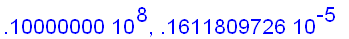
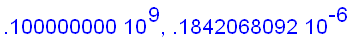
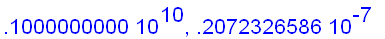
The examples above seem to suggest that we can find the limit
of those indeterminate forms by the limit
.
L'Hospital's Rule:
Suppose that f and g are differentiable and g ' ( x ) does not equal to 0 near a , except possibly at a . Suppose that
and
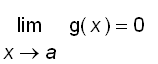
or
and
or
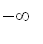
Then
.
If the limit on the right side exists (or is
or
).
Remarks :
1. L'Hospital's Rule is also valid for one-sided limits and for limit at infinity or negative infinity.
2. For the special case in which ,
and
, f ' and g ' are continuous, and
, it is not hard to see why l ' Hospital ' s Rule is true.
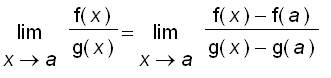
=
![[Maple OLE 2.0 Object]](images/suppl_LHospital101.gif)
=
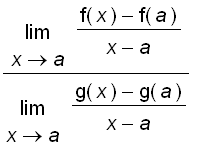
=
![[Maple OLE 2.0 Object]](images/suppl_LHospital103.gif)
=
![[Maple OLE 2.0 Object]](images/suppl_LHospital104.gif)
Geometrically, as we have seen in those examples above, the graphs of f and g look like their tangent at a if we zoom in towards the point (
). The equations of the tangent lines of
and
are
y = f( a ) + f ' ( a ) (
) = f ' ( a ) (
)
and
y = g( a ) + g ' ( a ) (
) = g ' ( a ) (
),
respectively.
This suggests visual that
=
.
Example:
.
Since
and
,
We can apply l' Hospital ' s Rule :
and
Since
,
we have
= 1.
Example:
.
Since
and
,
and
,
and
.
By l ' Hospital ' s Rule, we get
.
Example:
.
Since
and
,
=
and
(
) =
,
and
.
By l ' Hospital ' s Rule, we get
.
![[Maple Plot]](images/suppl_LHospital139.gif)
There are situations for which we have to use l ' Hospital ' s Rule more than once. For instance,
Example:
.
Note that
and
.
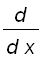
=
and
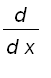
.
we have
again is an indeterminate form of type
, since
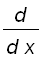
=
and
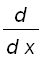
.
By l ' Hospital ' s Rule, we get
= 0,
and hence,
= 0.
![[Maple Plot]](images/suppl_LHospital157.gif)
Other type of indeterminate forms
(I). If
and
(or
), the limit
is called an indeterminate form of type
. We can deal with it by writing the product f g as a quotient :
or
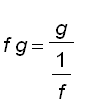
Example:
.
Note that
and
.
Writing
, we have
, so l ' Hospital ' s Rule gives
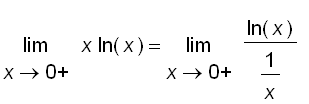
=
=
= 0
![[Maple Plot]](images/suppl_LHospital173.gif)
Note that another option is to write
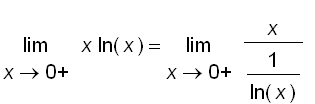
This gives an indeterminate form of type
, but if we apply l ' Hospital ' s Rule we get a more complicated expression than we started with. In general, we should choose the option that leads to simpler limit.
(II). If
and
, the limit
is called an indeterminate form of type
. We shall try to convert the difference into a quotient so that we have an indeterminate form of type
(or
).
Example:
.
Note that
and
.
Since
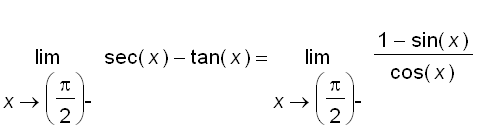
and
and
.
So we an indeterminate form of type
, l ' Hospital ' s Rule gives
= 0.
![[Maple Plot]](images/suppl_LHospital190.gif)
(III). Indeterminate Powers
(a) If
and
, the limit
is called an indeterminate form of type
.
(b). If
and
, the limit
is called an indeterminate form of type
.
(c). If
and
(or
), the limit
is called an indeterminate form of type
.
Each of these three cases can be treated by writing the function as an exponential :
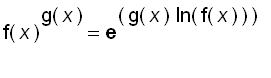
Example:
.
Note that this limit is an indeterminate form of type
, and we can write
as
.
We have shown that
,
since
is continuous at 0, we get
=
= 1.
Problems to think about :
1. Show that
, for all positive integer n . What does this imply ?
2. What's wrong with the argument below :
"
(again an indeterminate form of type
)
=
which does not exist !
Hence,
does not exist. "