¡@
Limit Laws
¡@
Limit Laws
Suppose that c is a constant and
and
. Then
¡@
(1).(Sum Law)
.
(2).(Scalar Multiple Law)
.
¡@
Remark :
From (1) and (2), we get
.
¡@
(3).(Product Law)
.
If we use the Product Law repeatedly with
, we obtain the following Law.
¡@
where n is a positive integer.
(4). If
, then
.
¡@
Remarks :
1. From (3) and (4), we get
(Quotient Law)
, if
.
¡@
2. Note that the condition
implies that g( x ) is bounded away from 0 for x near a . In fact, there exists a positive number d such that
whenever
and
. Hence,
is well-defined for
near a .
¡@
![[Maple Plot]](images_1/suppl_Limit_Laws19.gif)
Suppose that
, what can we say about the behavior of g( x ) near a ?
Intuitively,
implies that
can be as small as we want by taking x sufficiently close to a (but not equal to a ). Hence,
can be as large as we want by taking x sufficiently close to a (but not equal to a ). We would conjecture that
. Here is the proof :
Given M > 0, since
, there exists
, such that
whenever 0 <
.We get,
¡@
whenever 0 <
.
¡@
Hence,
.
¡@
¡@
Questions :
1. Suppose that both
and
exist, does
exist ?
2. Suppose that both
and
exist, does
exist ?
3. Suppose that
exists and
, does
exist ? If so, what is the limit ?
¡@
¡@
4. Suppose that c is a constant and
and
.
What can we say about the following limits ?
,
,
and
.
¡@
¡@
5. Suppose that
and
. What can we say about the following limits ?
,
,
and
.
¡@
Theorem If
when x is near a (except possibly at a ) and both
and
exist, then
¡@
.
¡@
Proof : Let
and
. Suppose that
.
¡@
¡@
![[Maple Plot]](images_1/suppl_Limit_Laws60.gif)
Taking
, we have that there exists
and
such that
¡@
whenever 0 <
,
¡@
and
¡@
whenever 0 <
.
Let
, if 0 <
then 0 <
and 0 <
, so we get
¡@
<
.
¡@
But this contradicts
. Thus, the inequality
must be false. Therefore,
.
¡@
Question : Suppose that
when x is near a (except possibly at a ) and both
and
exist, is it true that
¡@
?
The Squeeze Theorem
If
and
when x is near a (except possibly at a ) and
¡@
=
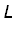
¡@
then
.
¡@
![[Maple Plot]](images_1/suppl_Limit_Laws86.gif)
Proof : Given
, since
=
, there exists
and
such that
¡@
whenever 0 <
,
and
¡@
whenever 0 <
.
¡@
Let
, if 0 <
then 0 <
and 0 <
, so we get
¡@
<
and
<
.
¡@
Therefore,
whenever 0 <
.
¡@
Example Show that
.
¡@
¡@
![[Maple Plot]](images_1/suppl_Limit_Laws107.gif)
Solution :
Note that since
does not exist, we can not use the Product Law.
Since
¡@
for all
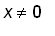
¡@
we have , as illustrated above,
¡@
and
for all
.
¡@
It is easy to show that
and
. By the Squeeze Theorem, we get
.
¡@
Question :
1. Suppose that
, is it true that
?
2. Suppose that
exists, is it true that
also exists ?
3. Suppose that
, is it true that
?
¡@
¡@
¡@
