The Mean Value Theorem

Download Maple Worksheet

Let f be an increasing function on and c be a number in 

( ), we have

for all x in .

 

If f ' ( c ) exists then f ' ( c ) is nonnegative.

 

If f is a differentiable function on , is the derivative of f always nonnegative ?

 

Here is another question : If a car travels 180 km in 1.5 hours, can we guarantee it will read 120 km/hr during the trip ?

 

At a first glance, these two questions seem to be irrelevant; however, they are a related to the following theorem :

 

The Mean Value Theorem  

If f is continuous on and differentiable in (), then there is a number c in () such that

f ' ( c ) =

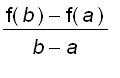
Or equivalently,  f ( b ) - f ( a ) = f ' ( c ) ( x - a ).

The Mean Value Theorem says that " For a given differentiable function over a given interval, the average rate of change over the interval equals the instantaneous rate of Change at some point in that interval".

Geometrically, this is what Mean Value Theorem means :

 

First, let's consider a special case for the Mean Value Theorem with f ( a ) = f ( b ) = 0.

 

Rolle's Theorem If f is continuous on and differentiable in

() such that f ( a ) = f ( b ), then there is a number c in () such that f '( c ) = 0.

 

If f is a constant then f ' ( x ) = 0, so c can be taken to be any number in ( ).

Recall that if f ' ( c ) = 0 then c is a critical number of f . Hence, f ( c ) may be a local extrema.

Now it comes the question:

" If f is a inconstant function which is continuous on and differentiable in () such that

f ( a ) = f ( b ),

is it true that f must have a local extrema in () ? "

By the extreme Value Theorem, f attains an absolute maximum and minimum values on .

The fact that f ( a ) = f ( b ) implies one of the absolute extrema must occur at some number c in ( ), that is, f ( c ) is a local extreme value of f . 

Since f '( c ) exists, by Fermat's Theorem, we get f ' ( c ) = 0.

 

The animation below illustrates the idea how to get the Mean Value Theorem from Rolle's Theorem.

 

 

Proof of the Mean Value Theorem

Let's take a look at the following animation to see how we can pull the graph of f such that the secant line joining the two endpoints become horizontal.

 

Consider the function

( )

Note that g is is continuous on and differentiable in 

( ) such that g( a ) = g ( b ).    By Rolle's Theorem, we get that there is a number c in ( ) such that g' ( c ) = 0. Since

g' ( x ) = f ' ( x ) - ,

we get

f ' ( c ) = .

 

Note:  If f does not satisfy the condition " f is continuous on and differentiable in ( ) ", then the conclusion in the Mean Value Theorem may not hold. Here are two examples :

 

(1)  Let on . 

It's not hard to see that f ( ) = f (1), but there does not exist c in such that f ' ( c ) = 0.

 

 

(2) Let on . 

Then

,

whereas g' ( x ) = and g' (1) does not exist ( g is not continuous at 1).   We see that there does not exist c in such that

g' (c) = .

 

Corollary:  If f , g are continuous on and differentiable in 

( ) such that  f ' ( x ) = g' ( x ) for all x in ( ), 

then 

f ( x ) = g ( x ) + C where C is a constant.

 

Proof It suffices to show that if f ' ( x ) = 0 for all x in ( ), then

f ( x ) = C for some constant C .

 

For each x in (], the Mean Value Theorem implies that there is a c in [] such that

f ( x ) - f ( a ) = f ' ( c ) ( x - a ).

 

Since f ' ( x ) = 0 for all x in (), f ( x ) = f ( a ). Therefore,

f ( x ) = f ( a ) for all x in .

 

We have seen that ( arcsin( x ) + arccos( x )) = 0 for all x in 

( ) and arcsin( x ) + arccos( x ) is continuous on . 

The Corollary above implies that

arcsin( x ) + arccos( x ) = C for some constant C .

 

Since

,

then . Therefore,

for all x in .

The significance of the Mean Value Theorem is that it enables us to obtain information about a function from information about its derivative. The following examples provide instances of this principle.

 

Example Suppose that f (0) = and f ' ( x ) 5 for all values of x . 

How large can f (2) be ?

 

We are given that f is differentiable everywhere and therefore f is continuous everywhere. We can apply the Mean Value Theorem on . There exists a number c that

f (2) - f (0) = f ' ( c ) (2 - 0)

So

f (2) = f (0) +2 f ' ( c ) (5) = 7

 

The largest possible value for f (2) is 7.

 

Example Determine the number of roots of .

First we notice that

< 0 and > 0.

 

By the Intermediate Value Theorem, we see that there exists a number c in such that .

The derivative of is

f ' ( x ) = .

Hence, f ' ( x ) > 3 for all x .

 

Using the Mean Value Theorem, we get if x > 0, then

 

= f ' ( ) ( ) for some between 0 and x .

Hence,

f ( x ) > f (0) + f ' ( ) ( ) > 5 for all x > 0.

Similarly, if x < , then

+ f ' ( ) ( ) for some between and x,

and so

< 0.

 

These say that f has no root outside .

 

Can f have more than one roots in ? If there exists a , b in such that

f( a ) = f( b ) = 0

By Rolle's Theorem, there exists a number c in ( ) such that 

f ' ( c ) = 0.  But f ' ( x ) > 3 for all x, we get a contradiction.

 

Therefore, f has exactly one root and the root is between and 0.

 

Example (Racetrack Principle) Let f and g be differentiable for all x in and suppose .

If f ' ( x ) g ' ( x ) for all x in then  

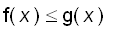
for all x in .

 

Let , then h is differentiable for all x in , and h ' ( x ) 0.

 

For each x in (], by applying the Mean Value Theorem to h on , we get

+ h' (c) ( ) 0.

Therefore for all x in .

Here are some problem to think about :

 

(1). If f ' ( x ) M for , is it always true that ?

 

(2). Is it true that for all x ?

 

(3). How do we know that ?

(4). Consider the functions

for and

 

f ' ( x ) = g ' ( x ) for all , yet f and g do not differ by a constant. Does this contradict to what we have discussed here ?

---

Download Maple Worksheet