¡@

The Precise Definition of a Limit

¡@

Formal definition of limit(f(x),x = a) = L .

¡@

We say that limit(f(x),x = a) = L , provided that

¡@

Given 0 < epsilon , there exists 0 < delta , such that abs(f(x)-L) < epsilon whenever 0 < abs(x-a) < delta .

¡@

We say limit(f(x),x = a) exists if there exists a real number L such that limit(f(x),x = a) = L .

¡@

Remark :

If limit(f(x),x = a) exists, then given 0 < epsilon , there exists 0 < delta , such that

abs(f(x[1])-f(x[2])) < epsilon whenever 0 < abs(x[1]-a) < delta and 0 < abs(x[2]-a) < delta .

¡@

Intuitively, if limit(f(x),x = a) exists, say L, then f(x[1]) and f(x[2]) can be as close as we want to L by taking both x[1] and x[2] sufficiently close to a (but not equal to a ). So f(x[1]) and f(x[2]) can be as close as we want by taking both x[1] and x[2] sufficiently close to a (but not equal to a ).

¡@

Proof of the remark :

Given 0 < epsilon , there exists 0 < delta , such that such that abs(f(x)-L) < epsilon/2 whenever 0 < abs(x-a) < delta . If 0 < abs(x[1]-a) < delta and 0 < abs(x[2]-a) < delta , then

abs(f(x[1])-f(x[2])) < abs(f(x[1])-L)+abs(f(x[2])-L... < epsilon/2+epsilon/2 = epsilon .

¡@

¡@

Example Show that limit(x^2,x = 1) = 1 .

Idea of the proof :

Given 0 < epsilon , we want to find 0 < delta , such that such that abs(x^2-1) < epsilon whenever 0 < abs(x-1) < delta .

¡@

[Maple Plot]

This tells us one way to find such a delta , we should solve the inequality abs(x^2-1) < epsilon . If abs(x^2-1) < epsilon , then 1-epsilon < x^2 < 1+epsilon . Assume further that epsilon < 1 , we get

¡@

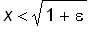
sqrt(1-epsilon) < x < sqrt(1+epsilon)

and so

¡@

sqrt(1-epsilon)-1 < x-1 < sqrt(1+epsilon)-1 .

¡@

¡@

[Maple Plot]

¡@

This implies that we should take delta to be the minimum of 1-sqrt(1-epsilon) and sqrt(1+epsilon)-1 .

¡@

Note that both 1-sqrt(1-epsilon) and sqrt(1+epsilon)-1 are positive, in fact sqrt(1+epsilon)-1 < 1-sqrt(1-epsilon) (why ?).

¡@

Proof : Given 0 < epsilon , without loss of generality may assume that epsilon < 1 , let

¡@

delta = min(1-sqrt(1-epsilon),sqrt(1+epsilon)-1) ( the minimum of 1-sqrt(1-epsilon) and sqrt(1+epsilon)-1 ).

¡@

If 0 < abs(x-a) < delta , then

¡@

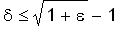
sqrt(1-epsilon)-1 <= -delta < x-1 < delta <= sqrt(1+epsilon)-1

Hence,

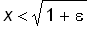
sqrt(1-epsilon) < x < sqrt(1+epsilon)

and so

1-epsilon < x^2 < 1+epsilon .

Therefore,

abs(x^2-1) < epsilon .

¡@

And the proof is completed.

¡@

Note that abs(x^2-1) = abs(x+1)*abs(x-1) , if abs(x-1) < 1 then abs(x+1) < 3 .

¡@

Alternative proof :

Given 0 < epsilon , let delta = min(1,epsilon/3) . If 0 < abs(x-1) < delta , then abs(x-1) < 1 . So we have abs(x+1) < 3 and

abs(x^2-1) = abs(x+1)*abs(x-1) < 3*epsilon/3 = epsilon .

¡@

¡@

Formal definition of limit(f(x),x = a) = infinity and limit(f(x),x = a) = -infinity .

¡@

We say that limit(f(x),x = a) = infinity , provided that

¡@

Given 0 < M , there exists 0 < delta , such that M < f(x) whenever 0 < abs(x-a) < delta .

¡@

We say that limit(f(x),x = a) = -infinity , provided that

¡@

Given 0 < M , there exists 0 < delta , such that f(x) < -M whenever 0 < abs(x-a) < delta .

¡@

¡@

Example Show that limit(1/((x-1)^2),x = 1) = infinity .

¡@

¡@

[Maple Plot]

Idea of the proof :

Given 0 < M , we want to find 0 < delta , such that such that M < 1/((x-1)^2) whenever 0 < abs(x-1) < delta .

Note that if M < 1/((x-1)^2) then 0 < (x-1)^2 < 1/M , which implies that 0 < abs(x-1) < 1/sqrt(M) .

Proof : Given 0 < M , let delta = 1/sqrt(M) . If 0 < abs(x-1) < delta = 1/sqrt(M) , then 0 < (x-1)^2 < 1/M .

So we have

M < 1/((x-1)^2) .

¡@

Download MapleWorksheet

¡@

¡@

¡@

¡@

¡@

¡@

¡@

¡@

¡@