Alternating Series
¡@
An alternating series is a series whose terms are alternately positive and negative. Namely, it has the form
or
where
.
Here are two examples :
1.
=
+ ... .
2.
+ ... .
3.
=
+ ... .
For the first and second examples, since
and
, by The Test for Divergence , both series diverge.
Let's take a look at the third example
=
+ ... .
Here we compute the nth partial sum
for
, 2, ... , 10 .
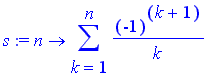
¡@
![S[1] := 1.](images/suppl_alternatingSeries16.gif)
![S[2] := .5000000000](images/suppl_alternatingSeries17.gif)
![S[3] := .8333333333](images/suppl_alternatingSeries18.gif)
![S[4] := .5833333333](images/suppl_alternatingSeries19.gif)
![S[5] := .7833333333](images/suppl_alternatingSeries20.gif)
![S[6] := .6166666667](images/suppl_alternatingSeries21.gif)
![S[7] := .7595238095](images/suppl_alternatingSeries22.gif)
![S[8] := .6345238095](images/suppl_alternatingSeries23.gif)
![S[9] := .7456349206](images/suppl_alternatingSeries24.gif)
![S[10] := .6456349206](images/suppl_alternatingSeries25.gif)
![S[11] := .7365440115](images/suppl_alternatingSeries26.gif)
![S[12] := .6532106782](images/suppl_alternatingSeries27.gif)
![S[13] := .7301337551](images/suppl_alternatingSeries28.gif)
![S[14] := .6587051837](images/suppl_alternatingSeries29.gif)
![S[15] := .7253718504](images/suppl_alternatingSeries30.gif)
![S[16] := .6628718504](images/suppl_alternatingSeries31.gif)
![S[17] := .7216953798](images/suppl_alternatingSeries32.gif)
![S[18] := .6661398242](images/suppl_alternatingSeries33.gif)
![S[19] := .7187714032](images/suppl_alternatingSeries34.gif)
![S[20] := .6687714032](images/suppl_alternatingSeries35.gif)
We have better picture of the series from the plot below.
![[Maple Plot]](images/suppl_alternatingSeries36.gif)
It seems that {
} is decreasing and {
} is increasing. It looks more clearly in the following plot, where {
} is plotted with red circles and {
} is plotted with blue circles.
![[Maple Plot]](images/suppl_alternatingSeries41.gif)
We can see from the graph above that {
} is increasing and bounded above by
, while {
} is decreasing and bounded below by
; by the monotonic Sequence Test, both {
} and {
} converge.
Moreover,
![S[2*n] = S[2*n-1]-1/(2*n)](images/suppl_alternatingSeries48.gif)
it follows that
. Therefore,
converges.
In general, we have the following theorem :
The Alternating Series Test
If
and {
} is decreasing with
, then the alternating series
( or
)
converges.
In fact,
= (
) + (
) + ... + (
)
since {
} is decreasing, we have
and {
} is decreasing.
But we can also write
=
- ... - (
) -
![b[2*n]](images/suppl_alternatingSeries66.gif)
¡@
so
for all n .
Therefore, by the Monotonic Sequence Theorem, {
} converges, say
.
Moreover,
and
, it follows that {
} converges and
= S
Therefore,
.
Note that
(Why ?).
In this case,
=
+ ... + ....
For each
,
+ ... + .... is also an alternating series which satisfies the assumption of the the Alternating Series Test. The following plot illustrates the case for
( the blue circle represents the point ( 41,
) ).
![[Maple Plot]](images/suppl_alternatingSeries82.gif)
It is therefore convergent, let's call the limit
, then we have
=
.
We say the series
is absolutely convergent if the series of absolute values
converges.
For example,
.
By the Integral Test,
converges, so
is absolutely convergent; and by the Alternating Series Test, we get that
is convergent also.
Note that the series
converges, but
diverges. From this, we see that a convergent series may not be absolutely convergent.
Question :
Is it true that if
is absolutely convergent then
is convergent ?
Let's examine the difference between the convergence of the series
and that of the series
.
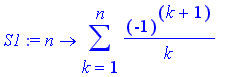
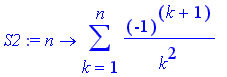
![[Maple Plot]](images/suppl_alternatingSeries100.gif)
It seems
converges much faster than
.
Now let's compare the convergence of the series
and
.
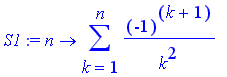
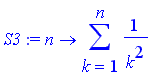
![[Maple Plot]](images/suppl_alternatingSeries107.gif)
The rate of convergence of these two series are about the same.
¡@
![[Maple Plot]](images/suppl_alternatingSeries108.gif)
From the graphs above, we see that the absolute value of the n th term of the series
goes to zero more rapidly than that of
.
It seems that we have a good reason to conjecture that if
is absolutely convergent then
is convergent.
Theorem If
is absolutely convergent then
is convergent.
Proof :
Note that
+
.
If
is absolutely convergent then
is convergent. So
is convergent. Therefore, by Comparison Test,
is convergent.
Since
, so
is the difference of two convergent series and is therefore convergent.
We say a series
converges conditionally iff
converges but
does not converge absolutely.
Now we have tests for positive terms and for alternating series. But what if the sign of the terms switches back and forth irregularly ? For example,
?
¡@
![S[1] := .5403023059](images/suppl_alternatingSeries127.gif)
![S[2] := -.2080734182](images/suppl_alternatingSeries128.gif)
![S[3] := -.3299974988](images/suppl_alternatingSeries129.gif)
![S[4] := -.1634109052](images/suppl_alternatingSeries130.gif)
![S[5] := .5673243710e-1](images/suppl_alternatingSeries131.gif)
![S[6] := .1600283811](images/suppl_alternatingSeries132.gif)
![S[7] := .1077003221](images/suppl_alternatingSeries133.gif)
![S[8] := -.1818750422e-1](images/suppl_alternatingSeries134.gif)
![S[9] := -.1012366958](images/suppl_alternatingSeries135.gif)
![S[10] := -.8390715291e-1](images/suppl_alternatingSeries136.gif)
![S[11] := .4023361807e-3](images/suppl_alternatingSeries137.gif)
![S[12] := .7032116322e-1](images/suppl_alternatingSeries138.gif)
![S[13] := .6980359857e-1](images/suppl_alternatingSeries139.gif)
![S[14] := .9766944157e-2](images/suppl_alternatingSeries140.gif)
![S[15] := -.5064586086e-1](images/suppl_alternatingSeries141.gif)
![S[16] := -.5985371752e-1](images/suppl_alternatingSeries142.gif)
![S[17] := -.1618607871e-1](images/suppl_alternatingSeries143.gif)
![S[18] := .3668426157e-1](images/suppl_alternatingSeries144.gif)
![S[19] := .5203708517e-1](images/suppl_alternatingSeries145.gif)
![S[20] := .2040410309e-1](images/suppl_alternatingSeries146.gif)
¡@
![[Maple Plot]](images/suppl_alternatingSeries147.gif)
¡@
![[Maple Plot]](images/suppl_alternatingSeries148.gif)
We have no clue !!!
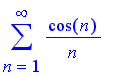
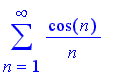
But it is rather different for the case if we consider the series
.
¡@
![[Maple Plot]](images/suppl_alternatingSeries152.gif)
![[Maple Plot]](images/suppl_alternatingSeries153.gif)
The series seems to converge !! We notice that the terms of the series
converges to 0 much faster than that of the series
and also
converges absolutely (why ??).
¡@
![[Maple Plot]](images/suppl_alternatingSeries157.gif)
Something funny about the plot for
--- It does not seem to be increasing ! Let's take a closer look.
![[Maple Plot]](images/suppl_alternatingSeries159.gif)
It's O.K. It is increasing. But can we be sure that
converge ?
Yes, since
converges absolutely, by the theorem,
converge.
Remark : If
converges, by the theorem,
converges. However, in general,
. Examples ???
¡@
¡@
¡@