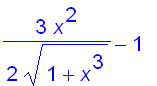¡@
Antiderivatives
Definition: A function F is called an antiderivative of f on an interval I if F ' ( x ) = f ( x ) for all x in I .
It is clear that if
is an antiderivative of f , and if
for some constant C , then
is also an antiderivative of f .
Is the converse true ?
Recall that we showed, by the Mean Value Theorem, if two functions have identical derivative on an interval I , then they must differ by a constant.
If both
and
are antiderivatives of f , then
' ( x ) =
' ( x ) = f ( x ).
so there exists a constant C such that
.
Theorem: If F is an antiderivative of f on the interval I , then all the antiderivatives of f on the interval I are of the form
where C is an arbitrary constant.
Suppose that
and
are antiderivatives of f and g , respectively, since
( cF + G ) ' = c f + g ,
we get that
is an antiderivative of
for all real number c .
Example: It is easy to check that for all x ,is an antiderivative of
and
is an antiderivative of
. Thus,
is an antiderivative of
. By the theorem, the antiderivatives of
are
, where C is an arbitrary constant.
![[Maple Plot]](images/suppl_antiderivative22.gif)
The notation
is traditionally used for an antiderivative of f (we shall see the reason later !!)
With this notation.
Given a function f on an interval I, does the antiderivative of f always exist ?
Theorem (Darboux)
Let
and I be an interval containing a , b .
Suppose that F ' ( x ) = f( x ) on I , and
.
If d is a number between f( a ) and f( b ), then there exists a number c in (
) such that
.
Proof: Without loss of generality, we may assume
. Let
, then H is differentiable so is continuous on I. By the Extreme Value Theorem, H has both maximum value and minimum value on
.
Since H ' ( a ) < 0 and H ' ( b ) > 0, we get that neither H( a ) nor H( b ) is the minimum value of H. This implies that there is a number c in (
) such that H( c ) is the the minimum value of H. Since H is differentiable on I , by Fermat's Theorem, we get
H ' ( c ) =
= 0.
That is,
.
Darboux's Theorem gives a necessary condition on f so that f has an antiderivative.
Example: Let
.
![[Maple Plot]](images/suppl_antiderivative35.gif)
We see that
,
and there exists no number c in (
) such that
. By Darboux's Theorem, f does not have an antiderivative.
We shall see later that if f is continuous on I , then f has antiderivatives. An equation that involves the derivatives of a function is called a differential equation . Given a function f on the interval I, the existence of antiderivatives of f is equivalent to the existence of solutions to the differential equation
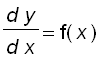
Hence, if f is continuous on I , then the differential equation above has solutions.
If we want to sketch the graph of the antiderivative F of
with
. We surely are guided by the fact that the slope of
is f( x ). We start at (
) and draw F as an increasing function since
for all
(why ??). To see whether the graph
has a point of inflection, we need to compute the derivative of f.
> diff( sqrt(1+x^3)-x , x );
solve( %=0 , x );
It would be a pain in the ass to solve f ' ( x ) = 0. And we could try all day to come up with a formula for the antiderivative of f and still in vain. Another possibility is to draw a graph of the tangent lines of
then use it to draw F as shown in the animation below :
![[Maple Plot]](images/suppl_antiderivative52/suppl_antiderivative52_001.jpg)
This works, we could get a more accurate graph using what is called a direction field .
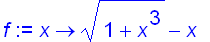
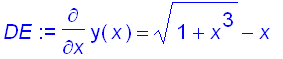
![[Maple Plot]](images/suppl_antiderivative55.gif)
![[Maple Plot]](images/suppl_antiderivative56.gif)
![[Maple Plot]](images/suppl_antiderivative57.gif)
Example: A particle moves in a straight line and has acceleration given by
. Its initial velocity is
cm/s and its initial displacement is
cm. Find its position function
.
Since v ' ( t ) =
, we have
![v(t) = 3*t^2+4*t+C[1]](images/suppl_antiderivative63.gif)
The fact that
gives
and so
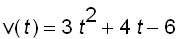
Since s ' ( t ) =
, we have
![s(t) = t^3+2*t^2-6*t+C[2]](images/suppl_antiderivative68.gif)
But we are given that
, so
and
.
![[Maple Plot]](images/suppl_antiderivative48.gif)