Continuity
A function
is continuous at
if
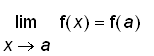
Intuitively speaking,
is continuous at
if
approaches
as
approaches
, as shown in the animation below :
![[Maple Plot]](images_1/suppl_continuity200510/suppl_continuity200510_001.gif)
If
is defined near
, we say
is discontinuous at
(or
has a discontinuity at
), if
is not continuous at
. How can
be discontinuous at
?
Case (i)
exists but
or
is not defined at
,for example
at
.
![[Maple Plot]](images_1/suppl_continuity200527.gif)
In this case, we say
has a removable discontinuity at
, because we can redefine
by
so that
is continuous at
.
Case (ii) Both
and
exist, but
, for example
if
and
if
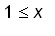
![[Maple Plot]](images_1/suppl_continuity200541.gif)
In this case,
has a jump discontinuity at
.
Case (iii) Either
or
does not exist, for example
.
![[Maple Plot]](images_1/suppl_continuity200547.gif)
Theorem If
and
are continuous at
and
is a constant, then the following functions are also continuous at
:
1.
2.
3.
4.
if
.
Note that from 1 and 2, we get that
is also continuous at
.
Since
for P , Q polynomials and
, any rational functions is continuous wherever it is defined.
We say
is continuous in an interval, if
is continuous at very number in this interval. Geometrically, we can think of a function that is continuous in an interval as a function whose graph has no break in it. In other words, the graph can be drawn without removing your pen from the paper.
Intermediate Value Theorem
Suppose that
is continuous on the interval
and let
be any number between
and
, where
. Then there exists a number
in (
) such that
.
![[Maple Plot]](images_1/suppl_continuity200573/suppl_continuity200573_001.gif)
The Intermediate Value Theorem says that if
, where
, are in the range of a continuous function
, then the interval
is contained in the range of
.
![[Maple Plot]](images_1/suppl_continuity200579/suppl_continuity200579_001.gif)
We can use the Intermediate Value Theorem to locate roots of equations as in the following example :
Consider the equation
, since
=
and
= 12
The Intermediate Value Theorem says that there is a number
in (
) such that
. In other words, the equation has at least one root in the interval (
). In fact, the Intermediate Value Theorem can help us finding the numerical values of these roots using bisecting algorithm .
The Inverse of a Continuous Function
From the animation below, it is not hard to believe that the inverse of a continuous function is also continuous.
![[Maple Plot]](images_1/suppl_continuity200589.gif)
Suppose that
is strictly increasing and continuous on
. Let
and
and let
be the inverse of
. Note that
is strictly increasing on
. Let
be a number in (
), to show
is continuous at
, we have to show that for each
> 0 there is a
> 0 such that
<
whenever
<
![y[0]+delta](images_1/suppl_continuity2005107.gif)
Let
, so that
. Suppose
is given, without loss of generality, we may assume that
is very small that both
and
are in
.
Let
, see the diagram below .
![[Maple OLE 2.0 Object]](images_1/suppl_continuity2005116.gif)
If
<
then
<
. Since is strictly increasing, we get
=
<
<
=
![g(y[0])+epsilon](images_1/suppl_continuity2005125.gif)
Therefore,
is continuous at
.
For each integer n , since
is continuous and increasing on [
), its inverse function
is also continuous on [
).
Question : Suppose that
is a one-to-one continuous function defined on
, is it true that
is monotonic on
(that is,
is increasing or
is decreasing on
) ?
The Intermediate Value Theorem can help us answer this question. Suppose that
is not monotonic on
, then there exist
in
with
<
<
such that
and
![f(c[3]) < f(c[2])](images_1/suppl_continuity2005147.gif)
or
and
![f(c[2]) < f(c[3])](images_1/suppl_continuity2005149.gif)
Without loss of generality, we may assume
and
. Let
be a number between
and
, the Intermediate Value Theorem says that there exist numbers
with
in (
),
in (
) such that
=
, as shown in the graph below, which contradicts to the fact that
is one-to-one. Hence,
is monotonic on
.
![[Maple Plot]](images_1/suppl_continuity2005165/suppl_continuity2005165_001.gif)
Assume that
and
is continuous at
.
Given
> 0, since
is continuous at
, there exists
> 0 such that
whenever
![abs(y-b) < delta[1]](images_1/suppl_continuity2005174.gif)
Since
, there exists
> 0 such that
whenever
<
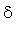
![[Maple OLE 2.0 Object]](images_1/suppl_continuity2005180.gif)
Hence, if
<
, we have
and then
. So, we have the following :
Theorem If
is continuous at
and
, then
. That is,
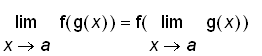
In other words, the limit symbol can be move through the function symbol.
Consequently, If
is continuous at
and
is continuous at
, then the composition function f o g is continuous at
.
Example Show that the function
is continuous on [
].
Solution :
Since
is continuous on on [
] ,
for all x in on [
] and
is continuous for all
. By the above theorem,
is continuous on [
].
Question : Suppose that
, f is defined at b and
exists, is it true that
?
The following example show that if we replace the continuity condition on f by the existence of
, then the above theorem will not be true even that f is well defined at b .
If
and
, then
. We get
and
.
Therefore,
.