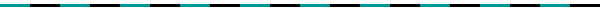How Derivatives Affect the Shape of a Graph

　

What Does f ' Say about f ?
Play with the animation below and observe how the derivative of the function affects the shape of its graph.

　

　

 

　

We see that on the part of the graph of f which is colored red, the tangent lines have negative slope and so f ' ( x ) < 0. While on the part of the graph of f which is colored blue, the tangent lines have positive slope and so f ' ( x ) > 0. It appears that f decreases when f ' ( x ) < 0 and increases when f ' ( x ) > 0. To prove that this is always the case, we use the Mean Value Theorem.

　

Increasing/Decreasing Test

(a) If f ' ( x ) > 0 on an interval ( ), then f is increasing on ( ).

(b) If f ' ( x ) < 0 on an interval ( ), then f is deceasing on ( ).

　

Proof

Let and be any two numbers in ( ) with . Since f is differentiable on , by the Mean Value theorem, there is a number c in ( ) such that

　

= f ' ( c ) ( )

　

If f ' ( x ) > 0 on an interval ( ), then the right hand side of the equation above is positive and so

　

> 0 or >

　

Thus, f is increasing.

　

If f ' ( x ) < 0 on an interval ( ), then the right hand side of the equation above is negative and so

　

or

Thus, f is increasing.

　

A consequence of Increasing/Decreasing Test is the following test.

　

The First Derivative Test Suppose that c is a critical number of a continuous function f.

(a) If f ' changes from positive to negative at c , then f has a local maximum at c .

(b) If f ' changes from negative to positive at c , then f has a local minimum at c .

(c) If f ' does not change sign at c , then f has no local maximum or minimum at c .

　

Example The function has a critical number at 0 ( ' (0) does not exist) and ' ( x ) changes from positive to negative at 0. So has a local maximum at 0.

　

Example The function has a critical number at 0 ( ' (0) = 0) and ' ( x ) changes from negative to positive at 0. So has a local minimum at 0.

　

Example The function has a critical number at 0 ( ' (0) = 0) but ' ( x ) does not change sign at 0. So has no local maximum or minimum at 0.

　

Let's revisit the following example.

Example Find the absolute maximum and minimum values of .

　

Note that

f ( x ) = for all , hence

f ' ( x ) = for all ,

f ( x ) = for all , hence

f ' ( x ) = for all ,

　

and f ' (0) does not exist (why ??).

Hence, the critical numbers of f are , 0, and .

　

We have f is increasing for all and 0 < , and f is deceasing for all < 0 and .

　

Since f ' changes from negative to positive at 0, f has a local minimum at 0. Since f ' changes from positive to negative at both and , f has a local maximum at both and .

　

Play with the animation below. Notice that the interval over which the graph of f is colored red, the curve lies below the tangents; while the interval over which the graph of f is colored above, the curve lies above the tangents.

　

 

　

Definition

If the graph of f lies above all of its tangent lines on an interval I, then it is called concave upward on I . If the graph of f lies below all of its tangent lines on an interval I, then it is called concave downward on I . A point P on a curve is called an inflection point if the curve changes from concave upward to concave downward or from concave downward to concave upward at P .

In the animation above, the graph of f is concave upward on the interval over which the graph of f is colored blue and the graph of f is concave downward on the interval over which the graph of f is colored red.

　

Also, we see that f ' ( x ) is decreasing (so f '' ( x ) < 0, why ?) on the interval over which of the graph of f is colored red. Whereas f ' ( x ) is increasing (so f '' ( x ) > 0, why ?) on the interval over which the graph of f is colored blue.

Now we would like to know how the first and second derivatives help to determine the intervals of concavity and inflection points.

Concavity Test

(a) If f '' ( x ) > 0 for all x in an interval I, then the graph of f is concave upward on I.

(b) If f '' ( x ) < 0 for all x in an interval I, then the graph of f is concave downward on I.

　

Proof

Let a be a number in I, the equation of the tangent line of at a is y = f ( a ) + f ' ( a ) ( ), so

　

f ( x ) -[ f ( a ) + f ' ( a ) ( )]= ( ) - f ' ( a ) ( ) .

　

By the Mean value Theorem, there exists a number c between x and a such that

　

= f ' ( c ) ( )

　

Hence

f ( x ) -[ f ( a ) + f ' ( a ) ( )] =( f ' ( c ) - f ' ( a )) ( ) .

　

　

If f '' ( x ) > 0 for all x in an interval I, by the Increasing/Decreasing Test, then f ' ( x ) is increasing on I.

(i) When , both f ' ( c ) - f ' ( a ) and are greater than 0, we have ( f ' ( c ) - f ' ( a )) ( ) > 0.

(ii) When , both f ' ( c ) - f ' ( a ) and are less than 0, we have ( f ' ( c ) - f ' ( a )) ( ) > 0.

　

Therefore, f ( x ) - [f ( a ) + f ' ( a ) ( )] is greater or equal to 0 on I.

　

This means that the graph of f lies above all of its tangent lines on I, that is, the graph of f is concave upward on I.

　

If f '' ( x ) < 0 for all x in an interval I, by the Increasing/Decreasing Test, then f ' ( x ) is deceasing on I. In this case, f ' ( c ) - f ' ( a ) and are of opposite signs, we get

　

( f ' ( c ) - f ' ( a )) ( ) < 0.

　

Therefore,

f ( x ) - [f ( a ) + f ' ( a ) ( )] < 0.

　

This means that the graph of lies below the tangent lines on I, that is, the graph of f is concave downward on I.

　

We have just shown the following :

(a) If f ' ( x ) is increasing on I, then the graph of f is concave upward on I.

(b) If f ' ( x ) is decreasing on I, then the graph of f is concave downward on I.

　

In fact, one can show that

(c) If the graph of f is concave upward on I , then f ' ( x ) is increasing on I .

(d) If the graph of f is concave downward on I, then f ' ( x ) is decreasing on I .

　

If ( c , f( c )) is an inflection point on the graph of f , by definition, the graph of f changes concavity at c . So for x near c ,

either

f ' increases for and f ' decreases for

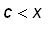
or

f ' decreases for and f ' increases for .

　

This implies that f ' has a local extrema at c . Hence, by Fermat's Theorem, c is a critical number of f ' , that is, f '' ( c ) does not exist or f '' ( c ) = 0.

　

However, f '' ( c ) does not exist or f '' ( c ) = 0 does not imply ( c , f( c )) is an inflection point . Examples??

　

If f '' ( c ) does not exist or f '' ( c ) = 0 , can you come up with a condition on f ' (or f '' ) so that ( c , f( c )) is an inflection point ?

　

The Second Derivative Test Suppose that f '' is continuous near c .

(a). If f ' ( c ) = 0 and f '' ( c ) > 0,then f has a local minimum at c .

(b). If f ' ( c ) = 0 and f '' ( c ) < 0,then f has a local maximum at c .

　

Geometrically, it is not hard to see why the test is true. For instance, if f '' ( c ) > 0, the continuity of f '' implies that f '' ( x ) > 0 for x near c , then f is concave upward near c. This means that the graph of f lies above its horizontal tangent line at c and so f has a local maximum at c .

　

　

In the algebraic point of view,

　

f ' ( x ) = f ' ( x ) - f ' ( c ) = f '' ( a ) ( ) for some a between x and c .

　

If f '' ( x ) > 0 for x near c , then f ' ( x ) < 0 for and f ' ( x ) > 0 for . Hence, by the First derivative test, f has a local minimum at c .

　

　

　

Example Sketch the graph of the function .

　

Using differentiation rules, we have

　

f ' ( x ) = f '' ( x ) =

　

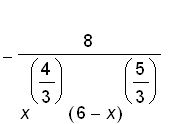
Since f ' (4) = 0 and f ' ( x ) does not exist at 0 and 6, the critical numbers are 0, 4, 6.

　

　

When , f ' ( x ) < 0, f is decreasing.

When 0 < , f ' ( x ) > 0, f is increasing.

When 4 < , f ' ( x ) < 0, f is decreasing.

When , f ' ( x ) < 0, f is decreasing.

　

We can apply the Second Derivative Test to tell that f has a local maximum at 4 (since f '' (4) < 0), but we need to use the First Derivative Test to determine whether f has a local maximum or minimum at 0 and 6. Since f ' changes from negative sign to positive sign at 0, f has a local minimum at 0. Whereas f ' does not change sign at 6, so f has no local maximum or minimum at 6.

　

　

When , f '' ( x ) < 0, the graph of f is concave downward.

When 0 < , f '' ( x ) < 0, the graph of f is concave downward.

When , f '' ( x ) > 0, the graph of f is concave upward.

　

Hence, (6, f(6)) is an inflection point.(Note that the curve has a vertical tangent at 6.)

　

　

Here is the graph of f, f ' and f '' on the same screen.

　

Problem to think about :

(1). Is it possible for a continuous function to have two local maxima and no minimum ?

(2). Suppose that f is continuous on the interval and has only one critical point c . If f has a local maximum (or minimum) at c , does f( c ) have to be the absolute maximum (or minimum) value of f ?

　

(3). Suppose that f ''' is continuous near c . If f '' ( c ) = 0 and f ''' ( c ) 0, does f always have an inflection point at c ?

　

(4). Does there exist a function f such that f ( x ) < 0, f ' ( x ) < 0, f '' ( x ) > 0 for all x ?

Does there exist a function f such that f ( x ) > 0, f ' ( x ) < 0, f '' ( x ) > 0 for all x ?

　

(5). Suppose that f is twice differentiable, is there always an inflection point between two local extrema ? (6). Consider , how does the graph of vary as the value of c changes ?

　

(7). For what values of c is there a straight line that intersects the curve

　

　

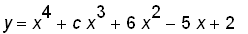
in four distinct points ?