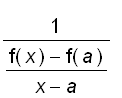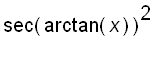Derivatives of Inverse Functions
Suppose that f is a one-to-one differentiable function, is its inverse g also differentiable ? Recall that if f is differentiable at x = a then the graph of f has a tangent line at ( a , f ( a )) and the slope of the tangent line is f ' ( a ). Let's take a look at the following animation :
![[Maple Plot]](images/suppl_diff_inverse1/suppl_diff_inverse1_001.jpg)
Since the graph of f and g are symmetric with respect to y = x , from the animation above, we see that the reflection of the tangent line to the graph of f at ( a , f ( a )) with respect to y = x is the tangent line to the graph of g at ( f ( a ), a ).
We know that the equation of the tangent line to the graph of f at
( a , f ( a )) is
y = f ( a ) + f ' ( a ) ( x - a ) ,
If f ' ( a ) does not equal to 0, then its reflection with respect to y = x is given by
y = a +(1/ f ' ( a )) ( x - f ( a )),
then g should be differentiable at ( f ( a ), a ) and
g' ( f ( a )) =1/ f ' ( a ), that is, g' ( b ) = 1/ f ' ( g ( b )) where b = f ( a ).
If f ' ( a ) = 0, the graph of f has a horizontal tangent at ( a , f ( a )),
and the reflection of a horizontal line with respect to y = x is a vertical line, then the graph of g has a vertical tangent at ( f ( a ), a ) and g is not differentiable at f ( a ).
In fact, it is not hard to verify this algebraically. Let y = f ( x ),
b = f ( a ), then g ( y ) = x , g ( b ) = a , and
=
Since g is continuous at b ( Why ?), we get x approaches a
(
) as y approaches b.
The fact
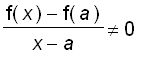
implies that
= 1/ f ' ( a )
Thus,
g' ( b ) = 1/ f ' ( g ( b ))
Another way to get the formula above, provided that g is also differentiable, is using the Chain Rule. By the definition of the inverse function, we have
f ( g ( y )) = y for all y in the domain of g
Differentiating both sides of the equation with respect to y , we get
f ' ( g ( y )) g' ( y ) = 1.
Thus, if f ' ( g ( y )) does not equal to 0, then
g' ( y ) = 1/ f ' ( g ( y )).
Derivatives of Inverse Trigonometric Functions
Recall that the function arcsin( x ) from [-1,1] to
is the inverse of the sine function with domain restricted to
. That is,
y = arcsin( x ) if and only if sin( y ) = x and y is in
.
Note that
=
for all x in (
), hence f ( x ) = arcsin( x ) is differentiable for all x in (
).
![[Maple Plot]](images/suppl_diff_inverse15.gif)
For all x in (
), by differentiating with respect to x both sides of the equation
sin( arcsin( x )) = x ,
we have
cos(arcsin( x ))
arcsin( x ) = 1
and
.
Since
> 0 for all
in (
), we get
=
.
Thus,
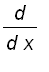
, for all x in (
).
Again, the function arccos( x ) from [-1,1] to
is the inverse of the cosine function with domain restricted to
. That is,
y = arccos( x ) if and only if cos( y ) = x and y is in
.
Note that
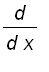
=
for all x in (
), hence f ( x ) = arccos( x ) is differentiable for all x in (
).
![[Maple Plot]](images/suppl_diff_inverse36.gif)
For all x in (
), by differentiating with respect to x both sides of the equation
cos( arccos( x )) = x ,
we have
arccos( x ) = 1
and
.
Since
> 0 for all
in (
), we get
=
.
Thus,
, for all x in (
).
Notice that
(arcsin( x ) + arccos( x )) = 0, what does this imply?
![[Maple Plot]](images/suppl_diff_inverse51.gif)
Similarly, the function arctan( x ) is the inverse of the function
y = tan( x ) with domain restricted to (
). That is,
y = arctan( x ) if and only if tan( y ) = x and y is in (
) .
Note that the lines
and
are vertical asymptotes of the curve y = tan( x ), and the lines
and
are horizontal asymptotes of the curve y = arctan( x ).
Since
=
for all x in (
),
y = arctan( x ) is differentiable for all real number x .
![[Maple Plot]](images/suppl_diff_inverse62.gif)
For all real number x , by differentiating with respect to x both sides of the equation
sin( arctan( x )) = x ,
we have
arctan( x ) = 1
and
.
Since
=
.
we get,
, for all x .
The derivatives of the remaining three inverse trigonometric functions are given below. The proofs of the formulas are left as exercises .
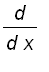
, for all x,
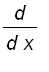
, for all
> 1,
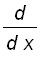
, for all
> 1.
Derivatives of Logarithmic Functions
Recall that
is an strictly increasing function and its inverse
is defined for all x > 0.
![[Maple Plot]](images/suppl_diff_inverse81.gif)
Since
> 0 for all x ,
is also differentiable for all x > 0 . For all x > 0, by differentiating both sides of the equation
,
we get
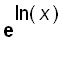
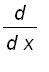
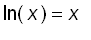
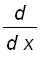
.
Hence ,
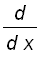
for all x > 0.
Let a be a positive number (
), by the Change of Base formula, we have
.
Hence,
is differentiable for all x > 0 and
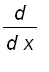
.
Logarithmic Differentiation
We have shown that for all rational number r ,

whenever the formula makes sense. Does the formula hold for irrational r ? If r is irrational, let's take a look how
is defined.
By Exponential laws, we have
, and so
for all x > 0. Therefore,
is differentiable for all x > 0 and
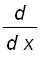
=
.
Finally, how is the function
defined and what is its domain ? Is it differentiable ? If so, what is its derivative function ?
For each x > 0, let
, so
and then
. Since both
and
are differentiable,
is differentiable and
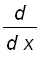
=
.
There is another way to calculate the derivative :
First, we take logarithms of both sides of the equation
, then
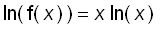
Differentiating both sides with respect to x gives :
f ' ( x ) =
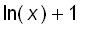
Solving for f ' ( x ), we have
f ' ( x ) = f ( x ) ( ln( x ) + 1) =
.
The method used above is called Logarithmic Differentiation, which is a powerful tool to calculate derivatives of complicated functions involving products, quotients or powers.
Example : Differentiate
.
First, we take logarithms of both sides of the equation and use the Laws of Logarithms to simplify :
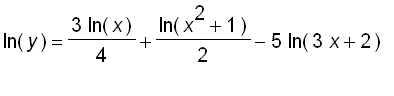
Differentiating both sides with respect to x gives :
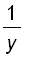
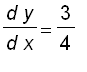
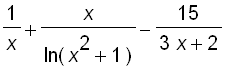
Solving for f ' ( x ), we have
(
).