¡@
Double Integrals and Iterated Integrals
First let's recall the basic facts about definite integrals of one-variable functions. If
is continuous for all
on [
], the definite integral of
on [
] is given by the limit of Riemann sums:
![int(f(x),x = a .. b) = limit(sum(f(c[i])*Delta*x,i = 1 .. n),n = infinity)](images/suppl_doubleInt6.gif)
where
and
is any point in [
] for all
, ...,
.
If
on [
],
represents the area of the region bounded by the graph of
,
,
and the
-axis.
![[Maple Plot]](images/suppl_doubleInt19/suppl_doubleInt19_001.jpg)
In a similar manner, we consider a function
of two variables continuously defined on a closed rectangle
![[Maple OLE 2.0 Object]](images/suppl_doubleInt21.gif)
and we first suppose that
. The graph of
is a surface with equation
. Let
be the solid that lies above
=
and under the graph of
, that is,
![[Maple OLE 2.0 Object]](images/suppl_doubleInt29.gif)
What is the the volume of?
If we take
on
x [
], here is the graph of
.
![[Maple Plot]](images/suppl_doubleInt35.gif)
Dividing the interval [
] into
subintervals [
] of equal length
and dividing the interval [
] into
subintervals [
] of equal length
, We divide the rectangle
into subrectangles
x [
]
of area
, where
,
. If we pick a sample point (
) in each
, then we can approximate
by "thin" rectangular columns.
The graph below shows the case where (
) is taken to be such that
is the minimum value of
over
:
![[Maple Plot]](images/suppl_doubleInt57.gif)
While the graph below shows the case where (
) is taken to be such that
is the maximum value of
over
:
![[Maple Plot]](images/suppl_doubleInt62.gif)
Notice that the sum of the volume of all these "thin" rectangular columns equals to
¡@
----- (1)
Note that the sum in (1) equals
![sum(sum(f(x[i*j],y[i*j])*Delta*y,j = 1 .. m)*Delta*x,i = 1 .. n) = sum(sum(f(x[i*j],y[i*j])*Delta*x,i = 1 .. n)*Delta*y,j = 1 .. m)](images/suppl_doubleInt64.gif)
As
and
go larger, the sum in (1) with
to be the maximum value of
over
gets smaller and the sum in (1) with
to be the minimum value of
over
gets larger, as shown in the animation below :
![[Maple Plot]](images/suppl_doubleInt73/suppl_doubleInt73_001.jpg)
![[Maple Plot]](images/suppl_doubleInt74/suppl_doubleInt74_001.jpg)
So we would expect the they eventually would reach the same value which should be the volume of
. In this case, no matter how we choose the sample point (
), the sum in (1) would still approach to volume of
. The animation below shows the case that (
) is taken to be (
) :
![[Maple Plot]](images/suppl_doubleInt80/suppl_doubleInt80_001.jpg)
So the volume of
equals to
![limit(sum(sum(f(x[i*j],y[i*j])*Delta*A,j = 1 .. m),i = 1 .. n),(m, n) = infinity) = limit(sum(sum(f(x[i*j],y[i*j])*Delta*A,i = 1 .. n),j = 1 .. m),(m, n) = infinity)](images/suppl_doubleInt82.gif)
Definition The double integral of
over the rectangle
is
![[Maple OLE 2.0 Object]](images/suppl_doubleInt85.gif)
if the limit exists. The sum
![[Maple OLE 2.0 Object]](images/suppl_doubleInt86.gif)
is called a double Riemann sum .
When f is a nonnegative function, the double integral
can be interpreted as the volume of the solid under the surface
and above the region R in the xy -plane. If f is not a nonnegative function, the double integral
can be can be interpreted as the "signed volume" (that means we take the volume of the solid above xy-plane to be positive and the volume of the solid under xy-plane to be negative) of the solid between the surface
and in the xy -plane over the region R .
Properties of Double Integrals
1.
.
2.
, where
is a constant.
3. If
for all (
) in R, then
.
How to compute the double integrals ?
Suppose that
is continuous over
x [
] (so for each
in [
],
is continuous, for all
in [
].). For each
in [
], we can define
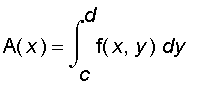
Note that
is continuous on [
].
If we now integrate the function
with respect to
from
to
, we get
![int(A(x),x = a .. b) = int([int(f(x,y),y = c .. d)],x = a .. b)](images/suppl_doubleInt114.gif)
The integral above is called an iterated integral . Usually, the brackets are omitted. Thus,
![int(int(f(x,y),y = c .. d),x = a .. b) = int([int(f(x,y),y = c .. d)],x = a .. b)](images/suppl_doubleInt115.gif)
Similarly, the iterated integral
![int(int(f(x,y),x = a .. b),y = c .. d) = int([int(f(x,y),x = a .. b)],y = c .. d)](images/suppl_doubleInt116.gif)
Let
and
.
Recall that if
is continuous on
, the volume of
can be approximate by
.
![[Maple Plot]](images/suppl_doubleInt123/suppl_doubleInt123_001.jpg)
Fixed
,
, the volume of each thin slice, is approximately equal to
.
![[Maple Plot]](images/suppl_doubleInt127.gif)
So
is approximately equal to
,
as
goes to infinity, the right hand side of the above equation approaches
.
So we have
=
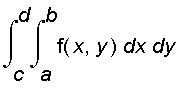
Similarly, the volume of
can be approximate by
.
![[Maple Plot]](images/suppl_doubleInt136/suppl_doubleInt136_001.jpg)
For fixed
, the volume of each thin slice is approximately equal to
.
![[Maple Plot]](images/suppl_doubleInt139.gif)
So
is approximately equal to
,
a s
goes to infinity, the right hand side of the above equation approaches
,x = a .. b) = int([int(f(x,y),y = c .. d)],x = a .. b)](images/suppl_doubleInt143.gif)
So we get
¡@
=
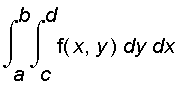
¡@
Fubini's Theorem
If f is continuous on the rectangle
x [
], then
=
=
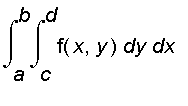
More generally, this is true if we assume that
¡@is bounded on
,
is discontinuous only on a finite number of smooth curves, and the iterated integrals exist.
¡@
Example: Evaluate the double integral
, where R = [
] x [
].
3DVIEW
![[Maple Plot]](images/suppl_doubleInt157.gif)
Note that the surface
¡@lies below the xy -plane, so the double integral
should be negative.
Solution : Fubini's theorem gives
¡@
=
=
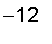
Example: Evaluate the double integral
, where R = [
] x [
].
Solution : We integrate with respect to x first,
¡@
=
= 0
Remarks :
1. If we integrate with respect to y first, the computation will be much more complicated.
2.
= 0 says that the volume of the solid under the surface
, above the xy-plane over
equals to of the solid above the surface
, below the xy-plane over
are equal.
Example: Find the volume of the solid S that is bounded by
, the planes
and
, and the three coordinate planes.
Solution : Note that is
positive on [
] x [
], so the volume equals to
=
![[int(x^2,x = 0 .. 2)]*[int(y,y = 0 .. 2)] = 16/3](images/suppl_doubleInt183.gif)
Note that in the special case where
and
x [
], the Fubini's theorem gives
=
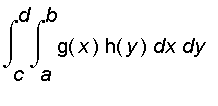
=
![int([int(g(x)*h(y),x = a .. b)],y = c .. d)](images/suppl_doubleInt189.gif)
=
![int(h(y)*[int(g(x),x = a .. b)],y = c .. d)](images/suppl_doubleInt190.gif)
=
![[int(g(x),x = a .. b)]*[int(h(y),y = c .. d)]](images/suppl_doubleInt191.gif)
![[Maple Plot]](images/suppl_doubleInt166.gif)
![[Maple Plot]](images/suppl_doubleInt174.gif)
![[Maple Plot]](images/suppl_doubleInt178.gif)