Maximum and Minimum Values
Some of the the most important applications of differential calculus are optimization problems.
For examples :
What is the shape of a can that minimizes manufacturing costs ?
What is the maximum acceleration of a space shuttle ?
These problems can be reduced to finding the maximum or minimum values of a function.
Definition : A function f has an absolute maximum at c if
for all x in D , where D is the domain of f . The number
is called the maximum value of f on D . Similarly, f has an absolute minimum at c if
for all x in D . The number
is called the minimum value of f on D . The maximum and minimum values of f are called the extreme values of f .
Definition: A function f has a local maximum at c if
when x near c . Similarly, f has a local minimum at c if
when x near c .
Example: The graph of the function
is shown below. We see that f has a local maximum at
, whereas the absolute maximum is
. Also, f has a local minimum at 0 and
is both a local and absolute minimum.
![[Maple Plot]](images/suppl_extreme_value11.gif)
The Extreme Value Theorem
If f is continuous on a closed interval
, then f attains an absolute maximum value and an absolute minimum value in
. That is, there exist c and d in
such that
and
for all x in
.
Remarks:
1. An extreme value can be taken on more than once. For example :
on
.
![[Maple Plot]](images/suppl_extreme_value20.gif)
2. If f is not continuous on a closed interval
, then f may not attain an absolute maximum value and an minimum value in
.
For example :
on
![[0, 2]](images/suppl_extreme_value24.gif)
![[Maple Plot]](images/suppl_extreme_value25.gif)
3.If f is continuous on a closed interval (
), then f may not attain an absolute maximum value and an minimum value in (
).
For example :
on (
).
![[Maple Plot]](images/suppl_extreme_value30.gif)
4.If f is continuous on an unbounded interval (for example : (
) ), then f may not attain an absolute maximum value and an minimum value on the interval.
For example :
on [
).
Given a continuous function f on [
], how to find its extreme values ?
1. The extreme values may occur at the endpoints (which is true for every monotonic functions).
2. If f has an extreme value at c in (
) then
must be a local extrema .
If
is a local extreme, the following animations show the possible situations that can happen :
![[Maple Plot]](images/suppl_extreme_value39/suppl_extreme_value39_001.jpg)
![[Maple Plot]](images/suppl_extreme_value41/suppl_extreme_value41_001.jpg)
![[Maple Plot]](images/suppl_extreme_value42/suppl_extreme_value42_001.jpg)
It seems that at the local maximum and minimum points either the tangent lines do not exist or the tangent lines are horizontal. The following theorem says that this is always true.
Fermat's Theorem
If f has a local maximum or minimum at c , and if f ' ( c ) exists, then f ' ( c ) = 0.
Proof: Suppose that f ' ( c ) exists, without loss of generality, we may assume f has a local maximum at c.
Then,
if x is sufficiently close to c . This implies that if x is sufficiently close to c and
, we have
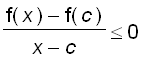
Thus,
.
Whereas, if x is sufficiently close to c and
, we have
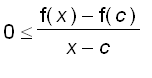
and hence
.
Since f ' ( c ) exists, we have
= f ' ( c )
and
f ' ( c ) =
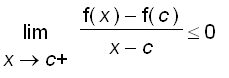
Therefore, f ' ( c ) = 0.
Definition: A critical number of a function f is a number in the domain of f such that f ' ( c ) does not exist or f ' ( c ) = 0.
Note that
may not be a local extrema if c is a critical number of f . For example, 0 is a critical number of
but f does not have a local extrema at
.
![[Maple Plot]](images/suppl_extreme_value55.gif)
Example Find the absolute maximum and minimum values of
on
.
![[Maple Plot]](images/suppl_extreme_value58.gif)
(1). Find all the critical numbers of f :
Since f ( x ) =
for all
, hence
f ' ( x ) =
for all
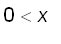
and f ( x ) =
for all
, hence
f ' ( x ) =
for all
.
Note that f ' (0) does not exist (why ??).
Therefore, all the critical numbers of f are 0,
and
.
(2). Find the values of f at the critical points and two endpoints :
f (0) = 0, f (
) = f (
) =
, f (
) =
, f (3) =
.
(3).Compare the values found in (2) :
f (
) = f (
) =
is the maximum value and f (3) =
is the minimum value of f .
Example: Find all the local and absolute extreme values of
on
.
![[Maple Plot]](images/suppl_extreme_value81.gif)
Since
g' ( x ) =
for all
and
g ' (0) does not exist, the critical numbers of g are
and 0. For all x in
,
and
, these imply that g has a local maximum at
and has a local minimum at
.
The values of of g at the critical numbers are
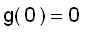
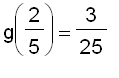
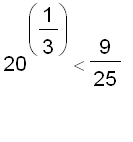
The values of of g at the critical numbers are
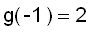
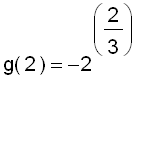
Comparing these four numbers, we see that the absolute maximum value is
and the absolute minimum value is
.
We leave it as an exercise for you to find all the local and absolute extreme values of
on
.
Here are some problems to think about :
Let f be a quadratic function
( i.e.
, where
).
(a). How many critical numbers can f have at most ?
Is it possible that f has no critical number ?
(b). How many local extreme values can f have at most ?
Is it possible that f has no local extreme value ?
(c). If f is a cubic function
(i.e.
, where
),
what are the answers to (a) and (b) ?
2003-11-17
![[Maple Plot]](images/suppl_extreme_value38/suppl_extreme_value38_001.jpg)
![[Maple Plot]](images/suppl_extreme_value40/suppl_extreme_value40_001.jpg)