¡@
Triple Integrals in Spherical Coordinates
Recall that the spherical coordinates (
) of a point
in space are shown below, where
is the distance from the origin
to
,
is the same angle as in cylindrical coordinates, and
is the angle between the positive z -axis and the line segment joining the origin and
.
The relationship between rectangular and spherical coordinates is given by the equations :
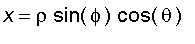
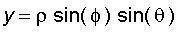
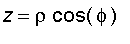
and
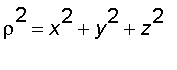
![[Maple Plot]](images/suppl_int_spherical13.gif)
In spherical coordinates system the counterpart of a rectangular boxes is a spherical wedge
![[Maple OLE 2.0 Object]](images/suppl_int_spherical14.gif)
as shown below :
It is sometimes difficult to evaluate the triple integral
using Cartesian coordinates. For example,
, where
is the unit ball:
= { (
) |
}
¡@
Note that in the spherical coordinates
![[Maple OLE 2.0 Object]](images/suppl_int_spherical22.gif)
Although we defined the triple integrals by dividing solids into small rectangular boxes, it can be shown that dividing a solid into small spherical wedges always gives the same result.
We can see from the figure above that the length of the navy line segment is
, the length of the green circular segment is
, and the length of the gold circular segment is
, where
.
If
,
, and
are small enough then the spherical wedge is approximately a rectangular box with dimension
,
,
. Hence an approximation of the volume of spherical wedge above is given by
.
¡@
So if we divide
into smaller spherical wedges
by means of equally spaced spheres
, half planes
, and half-cones
, then an approximation of the volume of
is
![Delta*V[i*j*k] = rho[i]^2*sin(phi[k])*Delta*rho*Delta*theta*Delta*phi](images/suppl_int_spherical41.gif)
and so
is approximately equal to
![sum(sum(sum(f(x[i*j*k],y[i*j*k],z[i*j*k])*Delta*V[i*j*k],i),j),k) = sum(sum(sum(f(x[i*j*k],y[i*j*k],z[i*j*k])*rho[i]^2*sin(phi[k])*Delta*rho*Delta*theta*Delta*phi,i),j),k)](images/suppl_int_spherical43.gif)
¡@
Therefore, we have
=
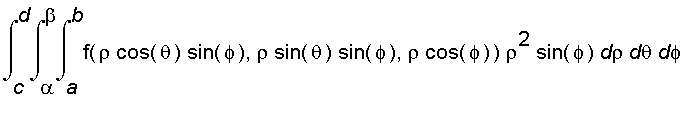
where
.
¡@
¡@
¡@
Now let's evaluate the integral
,
where
and
= { (
) |
}.
¡@
=
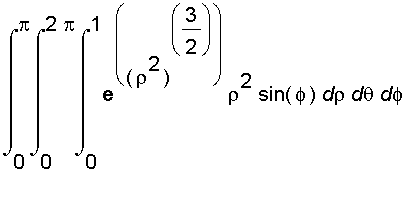
=
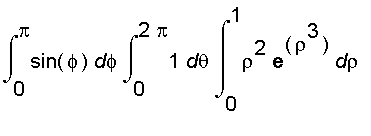
=
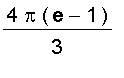
¡@
Note that it would have bee extremely difficult to evaluate the integral above without spherical coordinates. The iterated integral in rectangular coordinates would have been
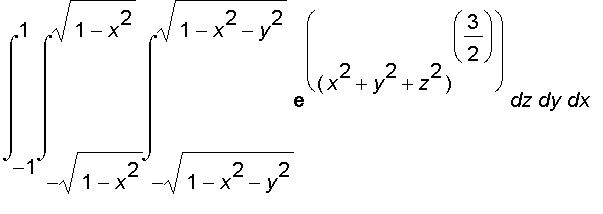
Now consider the solid that lies above the cone
and below the sphere
, as shown below. What is the volume of the solid ?
¡@
Notice that the sphere passes through the origin and has center (
) with radius
. And equation of the sphere in spherical coordinates is given by
or
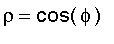
¡@
The cone can be written as
=
=
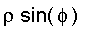
This gives
, or
. Therefore, the description of the solid in spherical coordinates is
![[Maple OLE 2.0 Object]](images/suppl_int_spherical69.gif)
![[Maple Plot]](images/suppl_int_spherical71/suppl_int_spherical71_001.jpg)
¡@
From the animations above, we see that the volume of the solid is
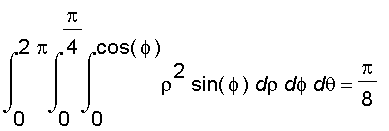
Download Maple Worksheet
![[Maple Plot]](images/suppl_int_spherical15.gif)
![[Maple Plot]](images/suppl_int_spherical23.gif)
![[Maple Plot]](images/suppl_int_spherical59.gif)
![[Maple Plot]](images/suppl_int_spherical70/suppl_int_spherical70_001.jpg)