Limits
We have learned that a line L is tangent to the circle at a point P if L passes through P perpendicular to the radius at P , as shown in the graph below.
![[Maple Plot]](images_1/suppl_limits20051.gif)
What does it mean to say a line L is tangent to some other curve C ? To define tangency for general curves, we need a dynamic interpretation of the tangency for a circle. The tangent line to a circle at a point P can be viewed as a result of the secant lines through P and near by points Q as Q moving toward P along the circle, as show in the animations below. (A line joining two points on the curve is a secant line to the curve.)
![[Maple Plot]](images_1/suppl_limits20052/suppl_limits20052_001.gif)
![[Maple Plot]](images_1/suppl_limits20053/suppl_limits20053_001.gif)
Suppose we want to find the equation of the tangent line to the parabola
at the point
. Since the tangent line passes through
, we will be able to to get the equation of the tangent line as soon as we know its slope
. The difficulty is that we need two points to compute the slope. However, we can compute an approximation to
by choosing a nearby point
, where
, on the parabola and compute the slope
of the secant line
.
![m[P*Q] = (x^2-1)/(x-1)](images_1/suppl_limits200513.gif)
![[Maple Plot]](images_1/suppl_limits200514.gif)
Here we compute the values of
for several values of
close to
.
![matrix([[x, m[PQ], x, m[PQ]], [1.500000000, 2.50000...](images_1/suppl_limits200518.gif)
It appears from the table above that the closer
is to
, the closer
is to
, the closer
is to
. It suggests that the slope of the tangent line should be
. (We shall discuss more about tangent lines in a later secession.)
![[Maple Plot]](images_1/suppl_limits200526/suppl_limits200526_001.gif)
![[Maple Plot]](images_1/suppl_limits200527/suppl_limits200527_001.gif)
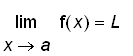
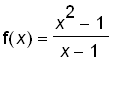 can get quite close to
can get quite close to
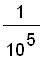 , how close to
, how close to
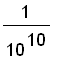 ?
?
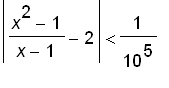 ( or
( or
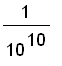 ) ?
) ?
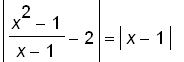
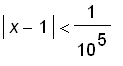 , that is, the distance from
, that is, the distance from
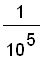 . For the second case, we can take
. For the second case, we can take
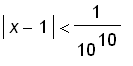 .
.
![[Maple Plot]](images_1/suppl_limits200565/suppl_limits200565_001.gif)
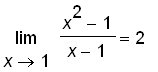
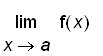 does not
depends whether
does not
depends whether
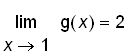
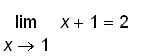
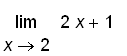 .
.
![[Maple Plot]](images_1/suppl_limits200585.gif)
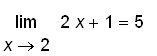
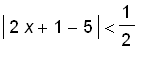 ?
?
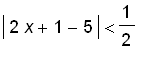 if and only if
if and only if
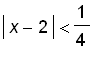 . That means we can take so that
. That means we can take so that
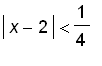 . Geometrically, we can also see this by the graph below.
. Geometrically, we can also see this by the graph below.
![[Maple Plot]](images_1/suppl_limits200596.gif)
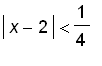
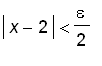 . Therefore,
. Therefore,
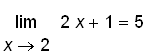 .
.
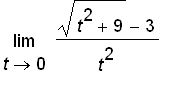 .
.
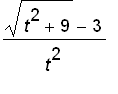 for several values of
for several values of
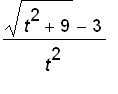 is even, we can take only positive values of
is even, we can take only positive values of
![matrix([[t, (sqrt(t^2+9)-3)/t^2], [.5000000000, .16...](images_1/suppl_limits2005113.gif)
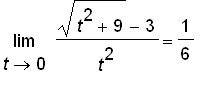
![matrix([[t, (sqrt(t^2+9)-3)/t^2], [.1000000000e-2, ...](images_1/suppl_limits2005119.gif)
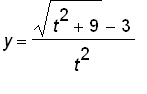 for
t
close to 0 within 0.01.
for
t
close to 0 within 0.01.
![[Maple Plot]](images_1/suppl_limits2005121.gif)
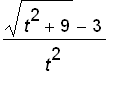 is not defined when
is not defined when
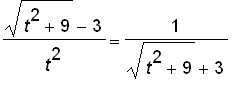 when
when
![matrix([[t, 1/(sqrt(t^2+9)+3)], [.1000000000e-2, .1...](images_1/suppl_limits2005128.gif)
![[Maple Plot]](images_1/suppl_limits2005129.gif)
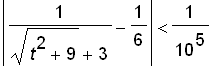
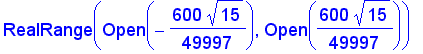
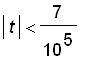 ( or even smaller). But this seems to be hard way to confirm that
( or even smaller). But this seems to be hard way to confirm that
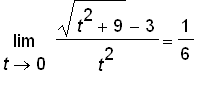
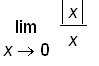 .
.
![[Maple Plot]](images_1/suppl_limits2005144.gif)
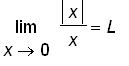 , for some number
, for some number
 exists.). Since the value of
exists.). Since the value of
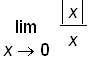 does not exist.
does not exist.
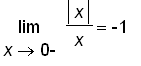 and
and
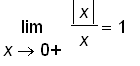
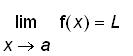 if and only if
if and only if
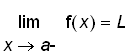 and
and
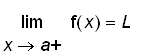
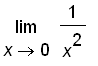 .
.
![matrix([[x, x^2, 1/(x^2)], [.1000000000, .100000000...](images_1/suppl_limits2005179.gif)
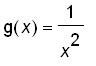 is an even function, we can just look at the values of
is an even function, we can just look at the values of
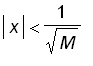 then
then
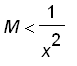 .That means the values of
.That means the values of
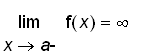
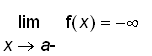
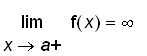
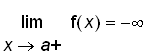
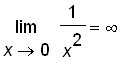 . Let's take a look at the graph of
. Let's take a look at the graph of
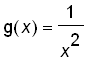 .
.
![[Maple Plot]](images_1/suppl_limits2005218.gif)
![[Maple Plot]](images_1/suppl_limits2005222.gif)
![[Maple Plot]](images_1/suppl_limits2005223/suppl_limits2005223_001.gif)
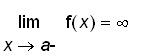
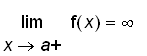
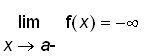
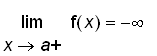
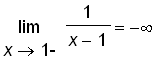 ,
,
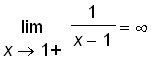 .
.
![[Maple Plot]](images_1/suppl_limits2005232.gif)
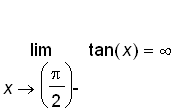 ,
,
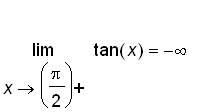 .
.
![[Maple Plot]](images_1/suppl_limits2005235.gif)
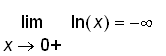 .
.
![[Maple Plot]](images_1/suppl_limits2005237.gif)