
Continuous Functions that Fail to Be Differentiable

¡@
¡@
We have seen that if
is differentiable at
, then
is continuous at
. Consequently, if
is not continuous at
then
is differentiable at
. For example :
¡@
if
and
if
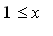
¡@
Since
is not continuous at
,
is not differentiable at
.
![[Maple Plot]](images/suppl_nondiff17.gif)
However, a function can be continuous at a point where its derivative does not exists. Here we describe the ways in which a continuous function can fail to be differentiable.
¡@
Recall that
is differentiable at
, if
exists.
¡@
Case (1) :
or
.
¡@
For example:
.
¡@
f is continuous at 0, and
=
.
¡@
Hence,
is not differentiable at
. Nevertheless, the graph of f has a tangent line at (0, 0) --- a vertical tangent line.
¡@
![[Maple Plot]](images/suppl_nondiff28/suppl_nondiff28_001.gif)
¡@
![[Maple Plot]](images/suppl_nondiff29/suppl_nondiff29_001.gif)
The graph of f near (0, 0) resembles a vertical line ---
.
¡@
![[Maple Plot]](images/suppl_nondiff31.gif)
¡@
Case (2) :
(
),
(
).
¡@
For example :
.
¡@
¡@
f is continuous at 0, and
=
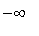
=
.
¡@
¡@
Hence,
is not differentiable at
and its graph has a sharp "cusp" at (0, 0). Nevertheless, the graph of f has a tangent line at (0, 0) --- a vertical tangent line.
¡@
![[Maple Plot]](images/suppl_nondiff43/suppl_nondiff43_001.gif)
¡@
![[Maple Plot]](images/suppl_nondiff44/suppl_nondiff44_001.gif)
¡@
Here is the graph of f near (0, 0).
¡@
¡@
![[Maple Plot]](images/suppl_nondiff45.gif)
¡@
Case (3): Both
and
exist, but
¡@
.
¡@
¡@
For example :
.
¡@
f is continuous at 0, and
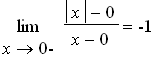
¡@
.
¡@
is not differentiable at
and its graph has a "corner point" at (0, 0) rather than a tangent line.
¡@
![[Maple Plot]](images/suppl_nondiff54.gif)
Here is the graph of f near (0, 0).
¡@
![[Maple Plot]](images/suppl_nondiff55.gif)
¡@
Case (4) : Either
or
does not exist.
¡@
For example :
, for all
, and
.
¡@
f is continuous at 0, and
does not exist.
¡@
![[Maple Plot]](images/suppl_nondiff62.gif)
Here is the graph of f near (0, 0).
¡@
![[Maple Plot]](images/suppl_nondiff63.gif)
In fact, the slopes of the secant lines oscillate between 1 and
infinitely often and so the graph of f does not have a tangent line at (0, 0).
¡@
![[Maple Plot]](images/suppl_nondiff65.gif)
¡@
Here some problems for you to think about :
1. Is there a function that is continuous everywhere and has "corner point" at each integer n , but is differentiable at every other point of the real line ?
¡@
2. Is there a function that is continuous everywhere and has a vertical tangent line at each integer n , but is differentiable at every other point of the real line ?
¡@
3. Suppose that the function f is continuous everywhere. At how many points do you suspect that f can fail to be differentiable ? What is the worst function you can think of ?
¡@
¡@
¡@