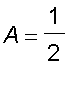¡@
Area in Polar Coordinates
Download Maple Worksheet
Suppose we want to find the area of the region
bounded by the polar curve
and by the rays
and
, where
is s positive continuous function and where
<
. We divide the interval [
] into subintervals with endpoints
,
,
, ... ,
and equal width
. The rays
then divide
into
smaller regions
with central angle
.
![[Maple Plot]](images/suppl_polarArea_new19.gif)
For each small region
, if we choose the sample point
* in the
-th subinterval [
], then the area
of
is approximated by the sector of a circle with central angle
and radius
(
* ).
![[Maple Plot]](images/suppl_polarArea_new29.gif)
Note that a typical sector of a circle with central angle
and radius
, as shown below, has area
.
![[Maple Plot]](images/suppl_polarArea_new33.gif)
Thus
=
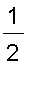
(
* )
, and so an approximation to the total area
of
is
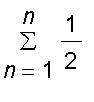
(
* )
,
which is a Riemann sum for the function
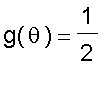
. It appears from the animation below that the approximation improves as
grows.
Therefore,
.
Example 1
Find the area enclosed by the four-leaved rose
.
![[Maple Plot]](images/suppl_polarArea_new52.gif)
Solution :
Notice that the desired area is
times the shaded area, which is swept out by a ray rotates from
to
. Therefore,
=
=
=
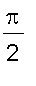
Example 2
Find the area of the region that lies inside the circle
and outside the cardioid
.
![[Maple Plot]](images/suppl_polarArea_new62.gif)
Solution :
These two curves intersect when
, which gives
. We see that they intersect at
and
. Hence the area inside the circle from
to
is given by
=
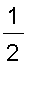
,
and the area outside the cardioid
to
is given by
=
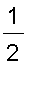
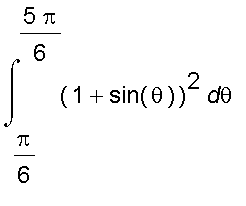
Thus the area we want is
, by symmetry about the vertical axis
, we have
=
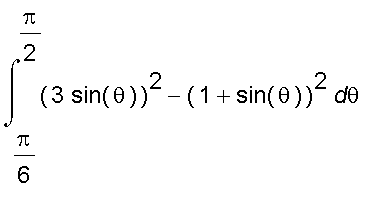
=
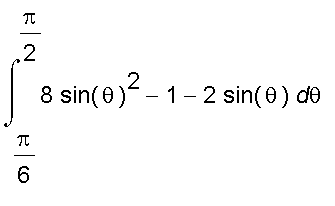
=
=
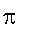
Download Maple Worksheet
![[Maple Plot]](images/suppl_polarArea_new48/suppl_polarArea_new48_001.jpg)