Rearrangement

¡@

If we rearrange the order of the terms in a finite sum, then of course the value of the sum remains unchanged.

Question : Is this the case for an infinite series ?

Let's first explore this question by looking at two examples, sum((-1)^(n+1)*1/n,n = 1 .. infinity) and sum((-1)^(n+1)*1/(n^2),n = 1 .. infinity) .

Let a[n] = (-1)^(n+1)*1/n , we know that sum(a[n],n = 1 .. infinity) = 1-1/2+1/3-1/4+1/5-1/6... + .... converges conditionally, say to S ( In fact, S = ln(2) ).

Does 1+1/3-1/2+1/5+1/7-1/4+1/9+1/11-1/6 + .... also converge to S ?

¡@

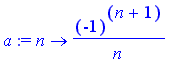
a := proc (n) options operator, arrow; (-1)^(n+1)/n...

¡@

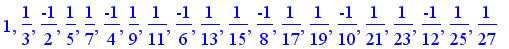
1, 1/3, -1/2, 1/5, 1/7, -1/4, 1/9, 1/11, -1/6, 1/13...

Let the n th terms of the series be b[n] and plot the partial sums of both series :

[Maple Plot]

sum(b[n],n = 1 .. infinity) = 1+1/3-1/2+1/5+1/7-1/4... + .... seems to converge to a larger sum.

Consider

1-1/2+1/3-1/4+1/5-1/6+1/7-1/8 + .... = S

In fact, if we multiply the series by 1/2 , we get

1/2-1/4+1/6-1/8+1/10-1/12+1/14-1/16 + .... = S/2

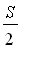
Inserting 0 between the terms of this series, we have

0+1/2+0-1/4+0+1/6+0-1/8+0+1/10+0-1/12+0+1/14+0-1/16... + .... = S/2

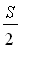
Add the series to

1-1/2+1/3-1/4+1/5-1/6+1/7-1/8+1/9-1/10+1/11-1/12+1/... + .... = S

We get

1+1/3-1/2+1/5+1/7-1/4+1/9+1/11-1/6+1/13+1/15-1/8 + .... = 3*S/2

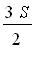
Let's now consider the series 1-1/2-1/4+1/3-1/6-1/8+1/5-1/10-1/12 + .... .

Let the n th terms of the series be c[n] and plot the partial sums of sum(a[n],n = 1 .. infinity) = sum((-1)^(n+1)/n,n = ... and sum(c[n],n = 1 .. infinity) :

¡@

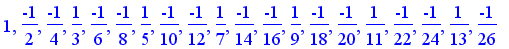
1, -1/2, -1/4, 1/3, -1/6, -1/8, 1/5, -1/10, -1/12, ...

¡@

[Maple Plot]

sum(c[n],n = 1 .. infinity) = 1-1/2-1/4+1/3-1/6-1/8... + .... seems to converge to a smaller sum.

Now let's turn to the series sum((-1)^(n+1)*1/(n^2),n = 1 .. infinity) .

Let a[n] = (-1)^(n+1)*1/(n^2) , we know that sum(a[n],n = 1 .. infinity) = 1-1/(2^2)+1/(3^2)-1/(... + .... converges absolutely, say to S .

Does 1+1/(3^2)-1/(2^2)+1/(5^2)+1/(7^2)-1/(4^2)+1/(9^2)+1... + .... also converge to S ?

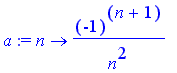
a := proc (n) options operator, arrow; (-1)^(n+1)/n...

¡@

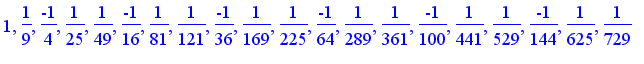
1, 1/9, -1/4, 1/25, 1/49, -1/16, 1/81, 1/121, -1/36...

Let the n th terms of the series be b[n] and plot the partial sums of both series :

¡@

[Maple Plot]

Let's now consider the series 1-1/(2^2)-1/(4^2)+1/(3^2)-1/(6^2)-1/(8^2)+1/(5^2)-1... + .... .

Let the n th terms of the series be c[n] and plot the partial sums of sum(a[n],n = 1 .. infinity) = sum((-1)^(n+1)/(n^2),... and sum(c[n],n = 1 .. infinity) :

¡@

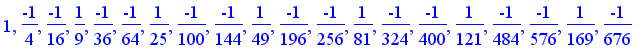
1, -1/4, -1/16, 1/9, -1/36, -1/64, 1/25, -1/100, -1...

¡@

[Maple Plot]

Quite different from the case for sum((-1)^(n+1)*1/n,n = 1 .. infinity) , both the series

1+1/(3^2)-1/(2^2)+1/(5^2)+1/(7^2)-1/(4^2)+1/(9^2)+1... + ....

and

1-1/(2^2)-1/(4^2)+1/(3^2)-1/(6^2)-1/(8^2)+1/(5^2)-1... + ....

seems to converge to S also.

Definition

A rearrangement of an infinite series sum(a[n],n = 1 .. infinity) is a series obtained by simply changing the order of the terms.

For example, both 1+1/3-1/2+1/5+1/7-1/4+1/9+1/11-1/6 + .... and 1-1/2-1/4+1/3-1/6-1/8+1/5-1/10-1/12 + .... are rearrangement of the series sum((-1)^(n+1)*1/n,n = 1 .. infinity) .

It turns out that

If sum(a[n],n = 1 .. infinity) is a absolutely convergent series with sum S ,

then any rearrangement of sum(a[n],n = 1 .. infinity) has the same sum S .

However, as we observed above, this is not true for any conditionally convergent series.

In fact, Riemann proved that

If sum(a[n],n = 1 .. infinity) is a conditionally convergent series and r is any real number,

then there is a rearrangement of that has a sum equal to r .

Download Maple Worksheet

¡@

¡@

¡@