Tangent Planes and Linear Approximations

Download Maple Worksheet

Recall that the equation of the tangent line to the curve at the point ( ) is given by

, where = f ' ( a )

provided that is differentiable at .  Moreover, the linear function

+ f ' ( a )( )

is a good approximation of near , in the sense that

 

Now consider a surface given by the equation and let be a point on . Does has a tangent plane at ? If so, what is the equation of the tangent plane ?

　

Let's consider the second question first. Suppose that has a tangent plane at and let be a curve on passing through . If is the tangent line to at then must lie on this tangent plane, as shown in the animation below.

 

In particular, let and be the curves obtained by intersecting the vertical planes and with the surface . Then the point lies on both and . Let and be the tangent lines to the curves and at the point . Then the tangent plane to the surface is the plane that contains both tangent lines and .

In terms of vector functions, and have the parametric equations

 

and ,

respectively .

　

so that and have direction vectors

u = ( ) and v = ( ),

respectively .

 

Hence a normal vector of the tangent plane is given by the cross product

u x v = ( )

 

so the equation of the tangent plane is given by

　

So we conclude that if has a tangent plane at then must have first order partial derivatives at ( ).

 

 

 

Here we consider the tangent plane to the paraboloid 

at  ( ).

Let , we have , and the equation of the tangent plane must be

3DView

3DView

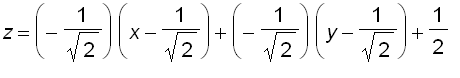
The graph above shows that the more we zoom in, the flatter the graph appears and the more it resembles its tangent plane.

 

In the graph below we corroborate this impression by zooming in toward the point () on a contour graph of .  Notice that the more we zoom in, the more the level curves look like equal spaced parallel lines, which is characteristic of a plane.

　

　

Therefore, in the view of visual evidence in the graphs above, the linear function

is a good approximation to when ( ) is near ( ).

　

The function is called the linearization of at ( ).

 

However, the existence of first partial derivatives is not sufficient to have tangent planes.

 

Here we provide an example that the function does have first partial derivatives but does not have a tangent plane :

Let for all ( ) except ( ) and .

 

We have and .

From the previous discussion, we know that if the surface has a tangent plane at ( ) then the equation of the tangent plane must be . However, the tangent line of the curve obtained by intersecting the vertical planes with the surface does not lie on .

3DView

We can confirm this by its contour graphs. As we zoom in toward ( ) on a contour graph of the function , the level curves do not look like equally spaced parallel lines at all.

 

 

When does the surface have a tangent plane at ( ) ?

 

We say is differentiable at ( ) iff

 

 

where .

 

Theorem

Suppose that has continuous first partial derivatives at ( ) then is differentiable at ( ).

 

If f is differentiable at ( ) iff the linearization at ()

 

is a good approximation of near ( ), that is, is close to when ( ) is close enough to ( ).

 

In particular, approaches to as ( ) approaches to ( ).

Hence, if is differentiable at ( ) then is continuous at ( ).

 

For the function , we have , are continuous for all in R . Hence, is differentiable for all in R.  In fact, if is a polynomial, then is differentiable for all in R .

 

For the function for all ( ) except ( ) and , we see that

=

 

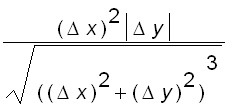
and that does not exist (Exercise !). Hence, g is not differentiable at ( ).

 

 

Note that both and are not continuous at ( ).

 

We shall see later that if has continuous first partial derivatives at ( ) then the surface have a tangent plane at ( ).