Vectors and the Geometry of Space

Download Maple Worksheet

 

A vector is a quantity (such as displacement or velocity or force) that has both magnitude and direction. A vector is often represented by an arrow. The length of the arrow represents the magnitude of the vector and the arrow points in the direction of the vector.

 

Sum of two vectors

The Triangle Law :

[Maple Plot]

The Parallelogram Law :

[Maple Plot]

Scalar Multiplication

If c  is a scalar and v  is a vector, then the scalar multiplication c v  is the vector whose length is abs(c) times the length of v and whose direction is the same as v  if 0 < c and is opposite to v if c < 0 .

If c = 0 or  v = 0 , then c v = 0 .

 

[Maple Plot]

For some purposes, it's best to introduce a coordinate system and treat vectors algebraically. If we place the initial point of a vector a  at the origin of the rectangular coordinate system, then the terminal point of a  has coordinates of the form ( a[1], a[2] ) or ( a[1], a[2], a[3] ), depending on whether our coordinate system is two- or three-dimensional. The coordinates are called the components of a  and we write

 

a = ( a[1], a[2] ) or a = ( a[1], a[2], a[3] ).

 

If a = ( a[1], a[2] ) and b = ( b[1], b[2] ), then

 

a + b = ( a[1]+b[1], a[2]+b[2] ) , c a = ( c*a[1], c*a[2] )

 

similarly, if a = ( a[1], a[2], a[3] ) and b = ( b[1], b[2], b[3] ), then

 

a + b = ( a[1]+b[1], a[2]+b[2], a[3]+b[3] ) , c a = ( c*a[1], c*a[2], c*a[3] )

 

The magnitude or length of the vector a = ( a[1], a[2] )  ( or ( a[1], a[2], a[3] ) ), denoted by | a | or ||a|| , is given by

 

||a|| = sqrt(a[1]^2+a[2]^2)   ( or sqrt(a[1]^2+a[2]^2+a[3]^2) , respectively.)

 

A unit vector is a vector whose is 1.

 

Let V[2] be the set of all two dimensional vectors and V[3] be the set of all three dimensional vectors.

Properties of Vectors

If a , b , and c are vectors in V[2] (or V[3] ) and c and d are scalars, then

1. a + b = b + a 2. a + ( b + c ) = ( a + b ) + c

3. a + 0 = a 4. a + (- a ) = 0

5. c ( a + b ) = c a + c b 6. ( c + d ) a = c a + d a

7. ( c*d ) a = c ( d a )

8. 1 a = a

 

Let  i = ( 1, 0 ) and j = ( 0, 1 ), then for all a = ( a[1], a[2] ), we have

a = a[1]i + a[2]j .

similarly, let i = ( 1, 0, 0 ) , j = ( 0, 1, 0 ) , k = ( 0, 0, 1 ) then for all a = ( a[1], a[2], a[3] ), we have a = a[1]i + a[2]j + a[3]k .

 

The Dot Product (or inner product)

If a = ( a[1], a[2] ) and b = ( b[1], b[2] ), then the dot product of a  and b is the number aĦE b given by

 

aĦE b = a[1]*b[1]+a[2]*b[2]

 

If a = ( a[1], a[2], a[3] ) and b = ( b[1], b[2], b[3] ), then the dot product of a and b is the number aĦE b given by

 

aĦE b = a[1]*b[1]+a[2]*b[2]+a[3]*b[3]

 

Properties of the Dot Product If a , b and c are vectors in V[2] (or V[3] ) and c is a scalar, then

1. aĦE a = a^2 where a = || a ||

2. aĦE b = bĦE a

3. aĦE ( b + c ) = aĦE b + aĦE c

4.c( aĦE b ) = ( ca ) ĦE b = aĦE ( cb )

5. 0ĦE a = 0

 

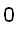
We can use Law of Cosines to get a nice geometric interpretation of the dot product.

Theorem : If theta is the angle between the vectors a and b , then

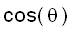
aĦE b = || a || || b || cos(theta)

 

Two vectors a and b are called perpendicular or orthogonal if the angle between them is Pi/2 . By the theorem, we have

a  and b are perpendicular  iff  aĦE b = 0 .

 

Hence, the vector 0 is perpendicular to all vectors.

 

Two vectors a and b are called parallel if the angle between them is 0 or Pi .

 

Projections : Let a and b be vectors in V[2] (or V[3] ).

The scalar projection of b onto a is

comp a b = aĦE b / || a ||.

 

The (vector) projection of b onto a is

proj a b = comp a b ( a / || a || ) = ( aĦE b / a^2 ) a, where a = || a ||.

 

The projection, or orthogonal component, of b perpendicular to a is

 

b `_|_` = b``-``Proj a b .

 

[Maple Plot]

Consider the case where a = ( -2, 3, 1 ) and b = ( 1, 1, 2 ),

 

then the projection of b onto a  is

( -3/7, 9/14, 3/14 )

 

and the orthogonal component of b perpendicular to a is

( 10/7, 5/14, 25/14 ).

[Maple Plot]

The Cross Product

If a = ( a[1], a[2], a[3] ) and b = ( b[1], b[2], b[3] ), then the cross product of a  and b is the vector

 

a x b = ( a[2]*b[3]-a[3]*b[2], a[3]*b[1]-a[1]*b[3], a[1]*b[2]... )

 

= ( a[2]*b[3]-a[3]*b[2] ) i + ( a[3]*b[1]-a[1]*b[3] ) j + ( a[1]*b[2]-a[2]*b[1] ) k

 

= det(MATRIX([[i, j, k], [a[1], a[2], a[3]], [b[1], b...

 

a x b is orthogonal to both a and b with direction given by the right-hand rule . If theta is the angle between a and b ( so theta is between 0 and Pi ), then

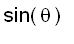
|| a x b || = ||a|| ||b|| sin(theta)

 

That is, the length of a x b is equal to the area of the parallelogram determined by a and b .

 

[Maple Plot]

Note that two nonzero vectors a and b are parallel if and only if a x b = 0 .

 

Properties of the Cross Product

If a , b , and c are vectors in V[3] and c is a scalar, then

1. Scalar Multiplication ( a a ) x ( b b ) = ab ( a x b )

 

2. Distributive Laws a x ( b + c ) = a x b + a x c

   ( b + c ) x a = b x a + c x a

 

3. Anti-Commutation b x a =``-``a x b

4. Non-Associative a x ( b x c ) = ( aĦE c ) b ``-`` ( aĦE b ) c

    ( a x b ) x c = ( aĦE c ) b ``-`` ( bĦE c ) a

 

5. a ĦE ( b x c ) = ( a x b ) ĦE c = det(MATRIX([[a[1], a[2], a[3]], [b[1], b[2], b[3]],...

 

The volume of the parallelepiped determined by the vectors a , b and c is

|| a ĦE ( b x c )||.

[Maple Plot]

Download Maple Worksheet