¡@
Directional Derivatives and the Gradient Vector
Consider the surface S with equation
and let
. Then the point
lies on S. What is the rate of change of
at (
) in the direction of an arbitrary unit vector u = (
) ?
Suppose the vertical plane that passes through P in the direction of u intersects S in a curve C . If C has a tangent line at P then the slope of the tangent line T to C at P is the rate of change of
in the direction of u , which is called the directional derivative of
at (
) in the direction of u , denoted by
.
Hence
,
if the limit exists.
¡@
Notice that for u = (
),
and for u = (
),
.
On the other hand, if we define a function g of single variable t by
,
then
g ' (0) =
=
.
If
is a differentiable function of
and
, by Chain Rule, we have
g ' ( t ) =
,
Put
, we get
.
¡@
So we have the following theorem :
Theorem
If
is a differentiable function of
and
, then
has a directional derivative in the direction of any unit vector u = (
) and
![D[u]*f(x,y) = f[x]*(x, y)*a+f[y]*(x, y)*b](images/suppl_directionalDerivatives31.gif)
Note that the theorem is also true if
is a differentiable function of three variables.
In terms of vector functions, the curve C obtained by intersection of the vertical plane that passes through P in the direction of u with S can be described by the vector function
F (t) = (
)
and the tangent vector T of C at P is given by
F '(0) = (
).
However,
the directional derivative
in the direction of u = (
) at (
) is the rate of change of
at (
) in the direction of u which is the third component of F '(0).
Let
,
be the curves obtained by intersection of the vertical planes
,
, respectively. Then the tangent vectors of
,
at P are
= (
) and
= (
), respectively.
The above theorem says that
, which also indicates that
,
,
lies on the same plane ( the tangent plane of S at P ).
![[Maple Plot]](images/suppl_directionalDerivatives54/suppl_directionalDerivatives54_041.jpg)
If
is a function of
and
, then the gradient of
is the vector function
defined by
, f[y](x,y))](images/suppl_directionalDerivatives61.gif)
So if
is differentiable, then
=
. u for any unit vector u .
If angle between u and
(
) is
, then we have
= |
(
) | | u |
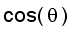
|
(
) |.
If
is a function of three variables, then the gradient of
is defined by
, f[y](x,y,z), f[z](x,y,z))...](images/suppl_directionalDerivatives78.gif)
and it is also true that if
is differentiable, then
f ( x ) =
( x )
u for any unit vector u .
Therefore, we have
Theorem
If
is a function of two or three variables, then the maximum value of the directional derivative
f( x ) is |
(x)| and it occurs when u has the same direction as
(x).
¡@
Let C is a level curve of f , suppose that C has the vector equation r (t) = (
), that is,
for some constant k . If
and f are all differentiable, by Chain Rule, we get
![F[x]](images/suppl_directionalDerivatives90.gif)
+
![F[y]](images/suppl_directionalDerivatives92.gif)
.
¡@
This says that the gradient vector
(
) is perpendicular to the tangent vector r ' (
) to C .
![[Maple Plot]](images/suppl_directionalDerivatives98.gif)
![[Maple Plot]](images/suppl_directionalDerivatives101.gif)
The gradient of a function
satisfies the following properties :
1.
points in the direction of maximum increase of the function.
2. |
| is the rate of increase of
in the direction of maximum increase.
3.
is perpendicular to each level curve of the function
.
4. |
| is inversely proportional to the spacing between the level curves.
Suppose S is a surface with equation
, that is, it is a level surface of a function F of three variables, let
be a point on S . Let C be a curve that lies on the surface S and passes through point P, say C is given by the vector function
r (t) = (
) with r (
) = (
) .
Since C lies on S , we have
.
Suppose that
and F are all differentiable, by Chain Rule, we get
![F[x]](images/suppl_directionalDerivatives116.gif)
+
![F[y]](images/suppl_directionalDerivatives118.gif)
+
![F[z]](images/suppl_directionalDerivatives120.gif)
,
that is,
. r ' ( t ) = 0 for all t.
¡@
In particular,
(
) . r ' (
) = 0.
This says that the gradient vector
(
) is perpendicular to the tangent vector r ' (
) to any curve C on S that passes through P .
If
(
) is a nonzero vector, then it is a normal vector of the tangent plane to S at P . In this case, the equation of the tangent plane is given by
.
The normal line to S at P , which is the line passing through P and perpendicular to the tangent plane, is given by the symmetric equations
=
.
¡@
Example Find the equation of the tangent plane and normal line at (
) to the ellipsoid
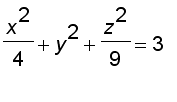
Note that the ellipsoid is a level surface of the function
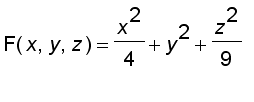
Therefore, we have
,
,
 = 2*z/9](images/suppl_directionalDerivatives142.gif)
,
,
 = -2/3](images/suppl_directionalDerivatives145.gif)
Hence the equation of the tangent plane is
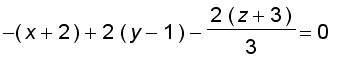
and the symmetric equations of the normal line are
=
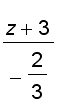
![[Maple Plot]](images/suppl_directionalDerivatives11.gif)
![[Maple Plot]](images/suppl_directionalDerivatives136.gif)