Lines and Planes in Space
A line
is determined by a point
on the line and the direction of
. The direction of
is conveniently described by a vector, so we let u be a vector parallel to
. Let
be an arbitrary point on
and let a and r be the position vectors of
and
then there is a number
such that
r = a + t u
which is a vector equation of
. Each value of the parameter
gives the position vector of a point on
(see the animation below).
![[Maple Plot]](images/suppl_linesANDplanes_3D14/suppl_linesANDplanes_3D14_001.jpg)
If a = (
), u = (
), r = (
), then the vector equation gives us the following parametric equations :
,
,
A plane in space is determined by a point
in the plane and a vector n , called normal vector , that is orthogonal to the plane. Let
be an arbitrary point in the plane and let a and r be the position vectors of
and
then
nĦE ( r
a ) = 0 .
If a = (
), n = (
), r = (
), then we get the scalar equation of the plane
![a*(x-x[0])+b*(y-y[0])+c*(z-z[0]) = 0](images/suppl_linesANDplanes_3D29.gif)
By collecting terms, we can rewrite the equation of the plane as
.
Two planes are parallel if their normal vectors are parallel and two planes are orthogonal if their normal vectors are orthogonal.
Let
be a point in the given plane
and let b be the vector from P to
, that is,
b = (
)
From the graph below, we see that the distance from
to to the plane is equal to the absolute value of the scalar projection of b onto the normal vector n = (
).
![[Maple Plot]](images/suppl_linesANDplanes_3D37.gif)
Thus, the distance
equals to | n ĦE b | / || n ||
=
![abs(a*(x[1]-x[0])+b*(y[1]-y[0])+c*(z[1]-z[0]))/sqrt...](images/suppl_linesANDplanes_3D39.gif)
=
![abs(a*x[1]+b*y[1]+c*z[1]-(a*x[0]+b*y[0]+c*z[0]))/sq...](images/suppl_linesANDplanes_3D40.gif)
=
![abs(a*x[1]+b*y[1]+c*z[1]+d)/sqrt(a^2+b^2+c^2)](images/suppl_linesANDplanes_3D41.gif)
Moreover, the point on that attains the distance
is
(
) (why ??).
Example
Find the point on the plane
that is closest to the point (
).
![[31/9, 10/9, 1/9]](images/suppl_linesANDplanes_3D46.gif)
Hence, (
) is the point on the plane
,
that is closest to the point (
).
Example
Find the distance between the parallel planes
and
.
Note that the planes are parallel because their normal vectors
(
) and (
)
are parallel. To find the distance
between the planes, we choose any point on one plane and calculate its distance to the plane. It is easy to see that (
) is on
.
By the distance formula, the distance from (
) to
is
.
So the distance between the planes is
.
Example
Find the distance between the lines
:
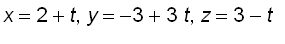
:
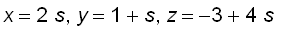
Since the two lines are skew, they can be viewed as lying on two parallel planes
and
. The distance between
and
is the same as the distance between
and
.
The common normal vector to both
and
must be orthogonal to both
u = (
) and v=(
).
So a normal vector is
![n := vector([13, -6, -5])](images/suppl_linesANDplanes_3D77.gif)
Put
in the equation of
, we get a point (
) on
and so the equation for
is
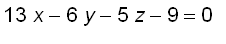
Since (
) is on
, so the distance between
and
is the same as the distance from (
) to
. That is,
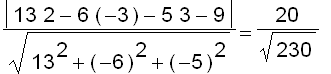
![[Maple Plot]](images/suppl_linesANDplanes_3D61.gif)
![[Maple Plot]](images/suppl_linesANDplanes_3D72.gif)