Motion in Space

Download Maple Worksheet

 

Motion of a Projectile

 

One of the most significant problems faced by the military is how to aim a projectile (e.g. a missile) so that it will end up hitting its intended target. Here we present the simplest possible case (where neither the target nor the source of the projectile are moving) in the following example.

 

A projectile is fired from an altitude meters above the ground with angle of ele vation and and initial speed . Assuming that air resistance is negligible and the only external force is due to gravity. What value of maximizes the range (the horizontal distance traveled) ?

 

Notice that here, the motion is in a single plane. We set up the axes so that the projectile starts at ( ). Since the force due to gravity acts downward, we have

 

F = m a = j

Thus

a = j .

Since v ' ( t ) = a , we have

v ( t ) = j + C ,

 

where C = v (0) = i + j .

 

Therefore

r ' ( t ) = v ( t ) = i + ( ) j

 

Integrating again, we obtain

r ( t ) = i + ( ) j + D .

 

But r (0) = D = h j , so

r ( t ) = i + ( ) j .

 

The parametric equations of the trajectory are therefore

 

 

The horizontal distance d is the value of x when . Setting , we get

 

 

Given , and , we can solve for by the quadratic formula.

 

 

For , we get or . The latter value of then gives

 

d = =

 

Clearly, has its maximum value when , that is, .

 

For m and m/sec , taking to be 9.8 m / :

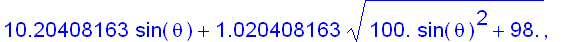
evalf(%/Pi*180);

 

 

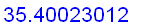
Hence has its maximum value when , that is, about 35.4 degree. The animation below shows how the trajectory changes with the angle of ele vation (in degrees).

 

 

A projectile of mass 1 kg is launched from ground level toward the east at 200 m/sec, at an angle of to the horizontal . If a gusting wind applies as a steady force of 2 newtons to the projectile. What is the landing location of the projectile and its speed at impact ?

 

Notice that because of the cross wind, the motion is fully three-dimensional. We orient the axes so that the positive y -axis points north, the positive x -axis points east and the positive z -axis points up, as shown below.

The two forces acting on the projectile are

 

gravity : in the negative z -direction with magnitude 9.8 m = 9.8 newtons

wind : in the y -direction with magnitude 2 newtons

 

Newton's second law gives that

a ( t ) = ( ).

Integration then gives us

v ( t ) = ( ) + v (0)

 

Note that the initial velocity is given by

v (0) = ( ) = ( ) .

Hence

v ( t ) = ( )

 

Integrating this, we get

r ( t ) = ( ) + r (0)

 

Taking the initial position to be the origin, we get r (0) = 0 , so that

 

r ( t ) = ( )

 

Now the projectile strikes the ground when the k component of position is zero, this occurs when

 

 

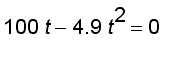
So the time of impact of the projectile is (about 20.4 seconds) and the speed of impact is | v ( ) | which is about 204 m/s.

 

Here we show a graph of the path of the projectile (red) with the shadow made by the path of the projectile (violet) on the ground.

3DIMAGE

Observe that the projection of the projectile's path onto the xz -plane is a parabola which is exactly the path of the projectile if there is no wind.

 

 

Circular Motion and Centripetal Force

 

Let's consider an object with mass m that moves in a circular path with constant angular speed . Then the position function is given by

 

r ( t ) = ( ) ,

 

and so the velocity function is given by

 

v ( t ) = r ' ( t ) = ( ) .

 

Notice that v ( t ) is orthogonal to r ( t ).

 

The acceleration function is given by

 

a ( t ) = v ' ( t ) = ( ) .

 

Therefore, Newton's Second Law gives the force as

F ( t ) = m a ( t ) = ( ) = r ( t )

 

The force acts in the direction opposite to the radius vector r ( t ) and therefore pointed toward the origin. Such a force is called a centripetal (center-seeking) force. Finally, observe that on this circular path,

 

| r ( t ) | = 1

so that at every point on the path, the force vector has constant magnitude .

 

Notice that the magnitude of the force increases as the angular speed increases. You have experienced this if you have been on a roller coaster with tight turns or loops. The faster you are going the stronger the force that your seat exerts on you.

 

 

 

Velocity and Acceleration

 

Suppose a particle moves in a helix path with position function

 

r ( t ) = ( ) ,

 

then the velocity function is given by

 

v ( t ) = r ' ( t ) = ( ) ,

 

and the acceleration function is given by

 

a ( t ) = v ' ( t ) = ( ) .

 

Here is an animation to show how the particle moves.

 

The acceleration vectors all point towards the z -axis.

 

 

If a moving particle starts at an initial position r (0) = ( ) with velocity v (0) = ( ) and its acceleration function is a ( t ) = ( ). How does the particle move ?

 

Since a ( t ) = v ' ( t ), vector integral gives us

 

v (t) = ( ) + C .

Putting , we have v (0) = C and so

v (t) = ( ) .

 

Again, since v ( t ) = r ' ( t ), vector integral gives us

 

r (t) =

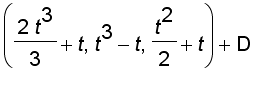
Putting , we have r (0) = D and so

 

r (t) = ( )

 

Here is an animation to show how the particle moves.

 

 

Curvature

 

Imagine that you are designing a highway system. Nearly all roads have curves, to avoid both natural and human-made obstacles. So that cars are able to maintain a reasonable speed on the roads, you need to design the roads in such a way so as to avoid curves that are too sharp. To do this, you will need to have some concept of how sharp a given curve is.

 

If C is defined by a continuously differentiable vector function r ( t ), we define its arc length function s by

s ( t ) = | r ' ( u ) | du

suppose that r ( t ) = x ( t ) i + y ( t ) j + z ( t ) k , then

 

 

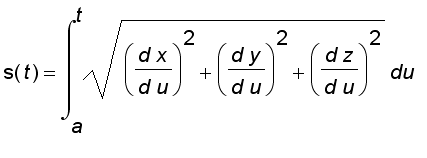
Thus, s ( t ) is the length of the part of C between r ( a ) and r ( t ). If we differentiate both sides of the equation above, we get

= | r ' ( t ) |

 

It is often useful to parametrize a curve with respect to arc length because arc length arises naturally from the shape of the curve does not depend on a particular parameter nor on a particular coordinate system.

 

For example, the helix r ( t ) = i + j + k , .

 

= | r ' ( t ) | = =

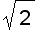
and so

s ( t ) = | r ' ( u ) | du = =

 

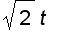
In this case, and we can reparametrize the helix with s by

r ( s ) = r ( t ( s )) = i + j + k

 

 

If C is a smooth curve defined by the vector function r ( t ) (that is, r ' ( t ) is continuous and r ' ( t ) does not equal to 0 for all t .) where is in [ ], then the unit tangent vector T ( t ) is given by

 

T ( t ) = r ' ( t ) / | r ' ( t ) |

and indicates the direction of the curve.

 

The curvature of C is

 

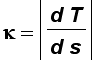
The curvature of C at a given point is a measure of how quickly the curve changes direction at that point (the larger the curvature the sharper the curve) and note that the curvature is independent of the parametrization.

 

By Chain Rule, we have

 

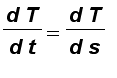
= | r ' ( t ) | and so = |T ' ( t )| / | r ' ( t ) |

 

It is easy to see that the curvature of a straight line is 0 , what is the curvature of a circle of radius ?

 

We can take the circle to have center the origin, and then a parametrization is

 

r ( t ) = i + j

 

Therefore

r ' ( t ) = i + j and | r ' ( t ) | = a

so

T ( t ) = i + j

and

T ' ( t ) = i j

This gives | T ' ( t ) | = 1, and

= | T ' ( t )| / | r ' ( t ) | =

 

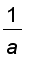
So a circle of radius has constant curvature .

 

Now let's find the curvature of a helix r ( t ) = i + j + k ,

 

 

| r ' ( t ) | = =

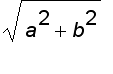
so

T ( t ) = i + j + k

and

T ' ( t ) = i j

 

This gives | T ' ( t ) | = and we get

 

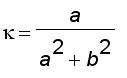
Hence the helix is also of constant curvature.

 

 

Tangent and normal components of Acceleration

 

Suppose a particle moves in the space with position vector function r ( t ), if we write v ( t ) = | r '( t )| = | v ( t )| for the speed of the particle, then

v ( t ) = v ( t ) T ( t )

 

If we differentiate both sides of this equation with respect to t , we get

 

a ( t ) = v' ( t ) T ( t ) + v ( t ) T ' ( t )

 

Since | T ( t ) | = 1 for all t , we notice that T ( t ) is orthogonal to T ' ( t ).

 

The unit normal vector is defined by

 

N ( t ) = T ' ( t ) / | T ' ( t ) |

So

a ( t ) = v' ( t ) T ( t ) + v ( t ) | T ' ( t ) | N ( t )

 

Since

= | T ' ( t )| / | r ' ( t ) | = |T ' ( t )| / v ( t )

 

this gives

a ( t ) = v' ( t ) T ( t ) + ( t ) N ( t )

 

We write and for the tangential and normal components of the acceleration, we have

 

a ( t ) = ( t ) T ( t ) + ( t ) N ( t )

 

where

= v' and =

 

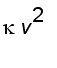
We can use this to explore a strategy for keeping the car on the road. From Newton's second law of motion, the net force acting on the car at any time t is

F ( t ) = m a ( t ) = m v' ( t ) T ( t ) + m ( t ) N ( t )

 

where m is the mass of the car.

 

Observe that if the normal component of the force, m ( t ), is too large, it may exceed the normal component of the force of friction between the tires and the road, causing the car to skid off the road. If the curve is sharp (that is, is large), notice that the only way to minimize the force applied in this direction is to make ( t ) small. So reducing speed is the only way to reduce the normal component of the force. Since T ( t ) points in the direction of the path of motion, you want to maximize the the tangent component of the force. In order to do that you need to make v' ( t ) as large as possible, that means you need to be accelerating while in the curve. So you should see now the optimal strategy for keeping your car on the road is reducing speed before you enter the curve and then gently accelerating once you are in the curve.

Download Maple Worksheet