¡@
Bessel Functions
![]()
Bessel function of
order ![]() is a solution to the differential equation (Bessel equation)
is a solution to the differential equation (Bessel equation)
![]()
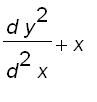
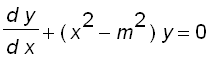
The Bessel functions are named after the German astronomer Friedrich Bessel (1784-1846). These functions first arose when Bessel solved Kepler's equation for describing planetary motion. These functions have been applied in many different physical situation, including the temperature distribution in a circular plate and the shape of a vibrating drumhead.
The Bessel function
of order 0 is defined by
 = sum((-1)^n*x^(2*n)/(2^(2*n)*n!^2),n = 0 ....](images/suppl_Bessel5.gif)
Let ![a[n] = (-1)^n*x^(2*n)/(2^(2*n)*n!^2)](images/suppl_Bessel6.gif) .
.
Then
![abs(a[n+1]/a[n]) = abs((-1)^(n+1)*x^(2*(n+1))/(2^(2...](images/suppl_Bessel7.gif)
=
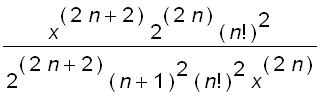
=
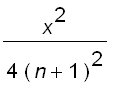 approaches to
approaches to ![]() for all
for all ![]()
Thus ,
by
Ratio test ,
the series converges for all values of
![]() . In other words, the domain of the Bessel function
. In other words, the domain of the Bessel function
![]() is
is ![]() .
.
Here are the first four partial sums and their graphs :
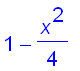
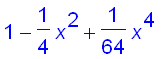
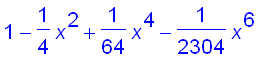
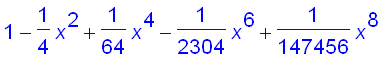
![[Maple Plot]](images/suppl_Bessel19.gif)
![[Maple Plot]](images/suppl_Bessel20.gif)
We see that
![]() , the Bessel function of order 0, is
an even function with
, the Bessel function of order 0, is
an even function with ![]() . Moreover, by the Alternating Series Estimation Theorem,
we have
. Moreover, by the Alternating Series Estimation Theorem,
we have
-sum((-1)^k*x^(2*k)/(2^(2*k)*k!^2),k = 0...](images/suppl_Bessel23.gif)
The animation below shows how the first 25 partial sums approach the Bessel function of order 0.
![[Maple Plot]](images/suppl_Bessel24/suppl_Bessel24_001.jpg)
The Bessel function
of order 1 is defined by
 = sum((-1)^n*x^(2*n+1)/(2^(2*n+1)*n!*(n+1)!...](images/suppl_Bessel25.gif)
Let ![b[n] = (-1)^n*x^(2*n+1)/(2^(2*n+1)*n!*(n+1)!)](images/suppl_Bessel26.gif) .
.
Then
![abs(b[n+1]/b[n]) = abs((-1)^(n+1)*x^(2*(n+1)+1)/(2^...](images/suppl_Bessel27.gif)
= 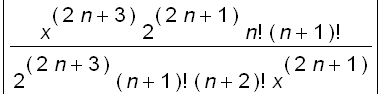
= 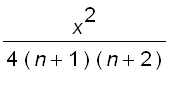 approaches to
approaches to ![]() for all
for all ![]()
Thus, by Ratio test,
the series converges for all values of ![]() . In other words, the domain of the Bessel function
. In other words, the domain of the Bessel function
![]() is also
is also ![]() .
.
Here is the graph of
![]() where
where ![]() .
.
![[Maple Plot]](images/suppl_Bessel37.gif)
We see that
![]() , the Bessel function of order 1, is
an odd function with
, the Bessel function of order 1, is
an odd function with ![]() .
.
The animation below
shows how the first 25 partial
sums approach ![]() .
.
Here we graph
![]() and
and ![]() on a common screen, can you see the relation between
them ?
on a common screen, can you see the relation between
them ?
![[Maple Plot]](images/suppl_Bessel44.gif)
It seems that
![]() , let's check.
, let's check.
 = sum((-1)^n/(2^(2*n)*n!^2),n = 0 .. infini...](images/suppl_Bessel48.gif)
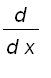
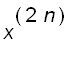
=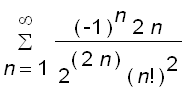
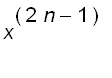
=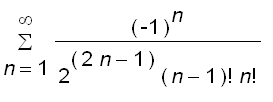
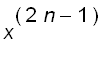
=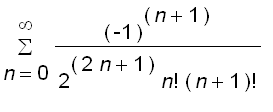
](images/suppl_Bessel56.gif)
To show that
![]() satisfies the equation
satisfies the equation
![]()
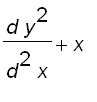
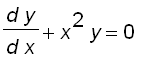
Let ![]() , we have
, we have
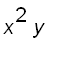 =
=![]()
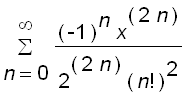
= 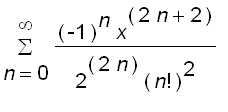
¡@
![]()
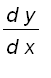 =
=
![]()
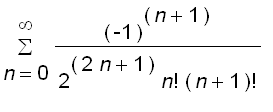
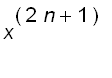
=
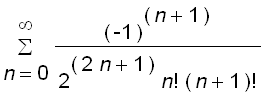
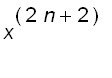
![]()
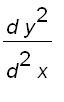 =
= ![]()
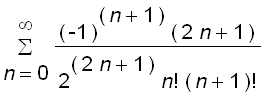
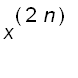
= 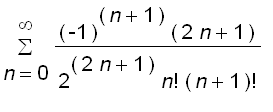
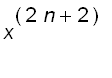
Thus,
![]()
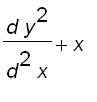
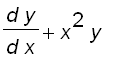 =
= 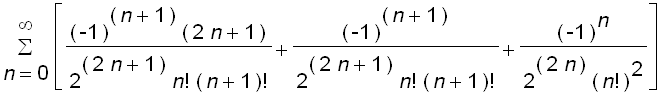
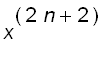
and
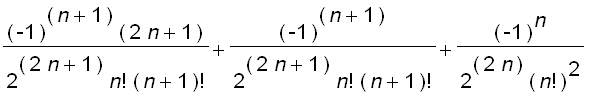
= 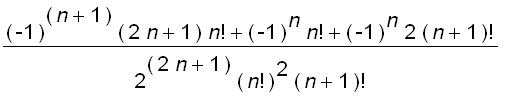 = 0
= 0
Therefore,
![]()
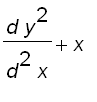
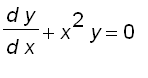 .
.
Similarly, we can
show that ![]() satisfies the equation
satisfies the equation
![]()
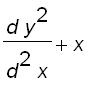
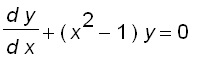
For more information about the Bessel functions and the Bessel equations, please refer to
¡@
http://mathworld.wolfram.com/BesselFunctionoftheFirstKind.html
¡@
![[Maple Plot]](images/suppl_Bessel41/suppl_Bessel41_001.jpg)