¡@

Tangent Lines and
Definition of the Derivative

 Previous   Download Maple Worksheet

Now let's look at another problem: how do we define the instantaneous velocity of a moving object?  To be precise, let's suppose that we have an object moving along the x-axis so that its position at any time is given by the expression .  For example, we might have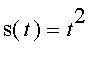, or . (  How does the object move in these two cases?  )

¡@

We can start by observing that there is no difficulty in defining the average velocity of the object during some time interval , using the elementary formula "Distance = Rate times Time".   The distance traveled during the interval is , and dividing by the elapsed time gives  Average velocity during the time interval = .

Here is a simple procedure to compute (decimal approximations to) average velocities:

> av := proc(s,t0,t1) evalf((s(t1) - s(t0))/(t1 - t0)) end proc:

¡@

We can now define a position function and compute average velocities. 

Example:

> s := t-> t^2 :
> av(s,1,5);

¡@

(You should check this result by hand.)  Of course, our problem is not to compute the average velocity over some time interval , but to compute the instantaneous velocity at some time . The solution is to compute the average velocities over shorter and shorter time intervals near .   Here are some examples with our last position function .

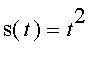t1	2	1.5	1.1	1.01
av( s, 1, t1 )	3	2.5	2.1	2.01

Experiment with a few more intervals, and convince yourself that the average velocity over a short time interval near is very close to 2.  Of course, we can never actually let .

Example:

> av(s,1,1);

Error, (in av) division by zero

¡@

but the point is that the average velocities behave nicely as approaches . We say that the average velocities have a limit  as approaches ,  and it makes sense to define the instantaneous velocity at to be this limit: 

Instantaneous velocity at time =  .

¡@

Now, this is exactly the same limit we saw in the tangent line problem. You can see this with a simple substitution: define a new variable by ,  so that , and the limit becomes Instantaneous velocity at time  = .

¡@

This suggests that we might be able to interpret the instantaneous velocity as the slope of the tangent line to some graph.  In fact, comparing the limits from our two problems, it is clear that the instantaneous velocity is the slope of the tangent line to the graph of the position function . Here is the picture for the position function 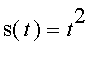that we were using above.  You should be able to see that the tangent line (red) at the point (1,1) has slope 2, as we would expect from our calculations of average velocity.

¡@

We say  is differentiable at , if exists, and the limit is called the derivative of (at ), and is denoted  '( ).

(  Maple uses the symbol D(f)  instead of '  )   Its geometric interpretation is the slope of the tangent line to graph of  at the point ( ,  ). 

If  represents the position of an object, then this limit represents the instantaneous velocity at time . These are both examples of the same idea:  the limit represents the instantaneous rate of change of the function .

Since the value of the limit will depend on , it is actually a function, and we will emphasis this by dropping the subscript and just writing

'( ) = .

¡@

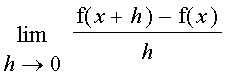Remark :  If  ( or ), by definition, is not differentiable at . However, the graph of  still has a tangent line at the point (  ,). In fact, the tangent line is vertical.

¡@

In the figure below, we can see that the graph of the function lies very close to the tangent line near the point of tangency.

¡@

In fact, by zooming in toward a point on the graph of a differentiable function,

we notice that the graph looks more and more like its tangent line.

¡@

Hence, it is reasonable to use the tangent line at ( ) as an approximation to the graph of when is near . This means that if it is easy to calculate a value of a function  , but difficult to compute nearby values of  , then we settle for the easily computed values of the linear function

L(x) = f(a) + f '(a)(x-a)

whose graph is the tangent line of  at ( ).  This approximation is called the linear approximation of at , and L(x) is called the linearization of  at .

For example, we may use the linearization of 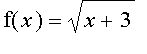to estimate .

¡@

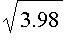f(1) = 2       f '(x) =        f '(1) = 1/4

=>  L(x) = f(1) + f '(1)(x-1) = (7+x)/4

=> = L(0.98) = 1.995

In the following table we compare the estimates from the linear approximation in the example above with the true values. Notice from this table that the linear approximation gives good estimates when close to but the accuracy of the approximation deteriorates when is farther from .

---

Previous   Download Maple Worksheet