Representations of Functions as Power series
Why do we want to express a known function as the sum of a power series ?
We will see later that this is a good strategy for integrating functions that don't have elementary antiderivatives (
or
for examples), for solving differential equations, and for approximating functions by polynomials. Scientists do this to simplify the expressions they deal with; computer scientists do this to represent functions on calculators and computers.
We now know that for
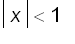
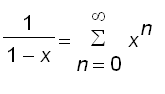
Moreover, we can compute the error of approximating
by the polynomial
= 1 + x + ... +
, using the following formula
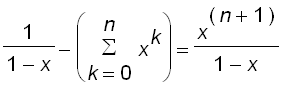
Clearly we can see from this formula and the animation below that
(1). For fixed
, the closer
is to
, the better
approximates
.
(2). For fixed
, the larger
is, the better
approximates
.
![[Maple Plot]](images/suppl_powerSeriesRep18/suppl_powerSeriesRep18_001.jpg)
We can use
------- (1)
to obtain power series representations for some other functions.
Algebraic manipulations ---- put the functions in the form of
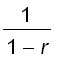
Example 1 Express
as the sum of a power series and find the intervals of convergence.
Replacing
by
in Equation (1), we have
=
=
=
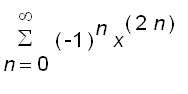
for
, that is,
. Therefore, the interval of convergence is (
). Of course, we can also determined the radius of convergence by ratio test, but that is unnecessary here. Because,
if and only if
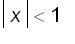
Play with the animation below and observe carefully.
Note that the function
is defined for all
, but the power series does not converge for
.
Example 2 Find a power series representation for
.
Put this function in the form of
as follows
=
=
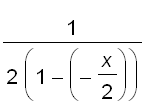
=
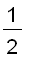
=
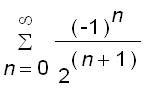
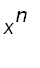
This series converges if and only if
, that is,
. So the interval of convergence is (
).
The animation below shows the convergence :
![[Maple Plot]](images/suppl_powerSeriesRep49/suppl_powerSeriesRep49_001.jpg)
Example 3 Find a power series representation for
.
Since
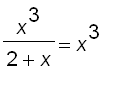
, all we have to do is to multiply the series by
.
=
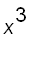
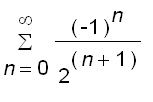
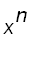
=
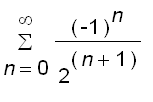
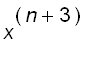
=
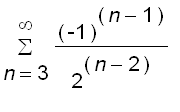
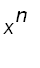
=
+ .....
The interval of convergence is also (
).
The animation below shows how the series converges :
![[Maple Plot]](images/suppl_powerSeriesRep64/suppl_powerSeriesRep64_001.jpg)
>
Differentiation and Integration
For
in the interval of convergence, we can differentiate or integrate a power series just as we would do for the polynomials ---- differentiate or integrate term-by-term .
Theorem If the power series
has radius of convergence
, then the function
defined by
![f(x) = sum(c[n]*(x-a)^n,n = 0 .. infinity)](images/suppl_powerSeriesRep69.gif)
is differentiable (and therefore continuous) on the interval (
) and
(i) f ' ( x ) =
=
+ ...
(ii)
=
+ ...
The radii of convergence of the power series in Equations (i) and (ii) are both
.
We called this differentiate or integrate term-by-term because that Equations (i) and (ii) can be rewritten in the form :
(iii)
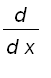
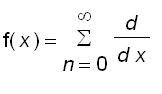
![c[n]*(x-a)^n](images/suppl_powerSeriesRep78.gif)
(iv)
![int(f(x),x) = sum(int(c[n]*(x-a)^n,x),n = 0 .. infi...](images/suppl_powerSeriesRep79.gif)
Example 4 Express
as the sum of a power series and find the interval of convergence.
Note that
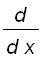
. Differentiating both sides of the equation
, we get
=
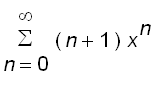
According to the theorem, the radius of convergence of the differentiated series is the same as the original series, namely,
. Since
diverges at
and
(take a good look at the animations below), we get that the interval of convergence of the series is (
).
The convergence for x in (
) :
![[Maple Plot]](images/suppl_powerSeriesRep92/suppl_powerSeriesRep92_001.jpg)
Example 5 Find a power series representation for
and find the interval of convergence.
Note that
, integrating both sides of
, we get
=
=
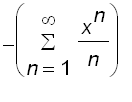
According to the theorem, the radius of convergence of the series is also equal to
. However, the series
converges at
and diverges at
. Therefore, the interval of convergence of the series is [
).
The convergence for x in (
) :
![[Maple Plot]](images/suppl_powerSeriesRep105/suppl_powerSeriesRep105_001.jpg)
The convergence for
:
![[Maple Plot]](images/suppl_powerSeriesRep107/suppl_powerSeriesRep107_001.jpg)
We have shown that
for all
in (
). From the animation above, we would conjecture that
for
, that is,
=
+.... .
In fact, it is true indeed. Since
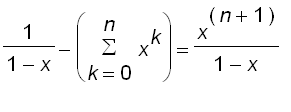
by integrating both sides of the equation above, we have
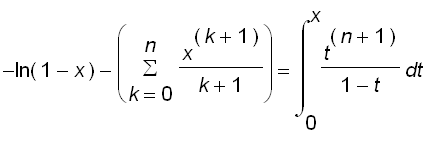
put
, we get
=
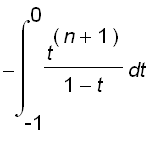
Since
and
for all
in
,
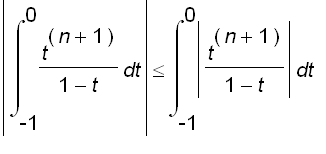
=
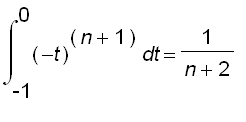
Therefore,
approaches
as
approaches
. This implies
=
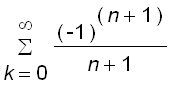
That is,
=
+ ......
Example 6 Find a power series representation for
and find the interval of convergence.
In Example 1, We have shown
=
for all
. We get
=
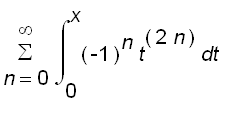
=
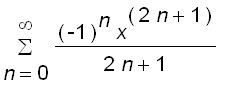
=
+ .......
for all
.
The convergence for x in (
) :
![[Maple Plot]](images/suppl_powerSeriesRep145/suppl_powerSeriesRep145_001.jpg)
Notice that the interval of convergence of the series
is [
].
We can show, as in Example 5, that
for all values of
in [
].
In particular, for
we get a formula to express
as an infinite series, namely
=
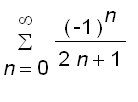
that is,
=
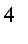
=
+ ......
Moreover, by the Alternating Series Estimation Theorem, we get
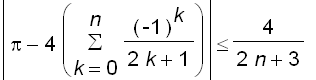
This gives us a good way to approximate
. If we want to find an approximation of
to 4 decimal places, we need to take
to be greater than
; we may take
, and the corresponding partial sum is about
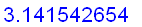
Not bad, right ?
Example 7 Approximate
correct to within
.
We first express the integrand,
, as the sum of a power series.
=
=
=
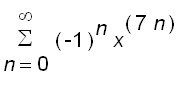
This series converges for
, that is, for
.
Since
, now we can integrate term by term :
=
=
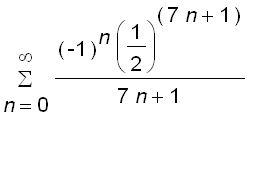
By the Alternating Series Estimation Theorem, we get
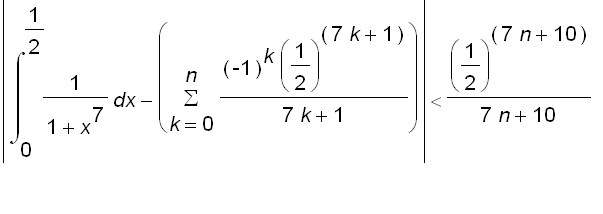
In order that the approximation is correct to within
, we need to take
so large that
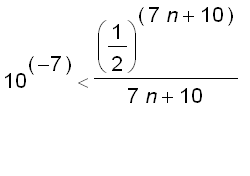
:

:

It suffices to take
, that is,
is approximately equal to
which is about
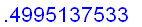
Power series center at
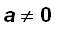
Example 8 Find a power series representation center at 1 for
and find the radius of convergence.
Since
, we can find the require series by integrating the power series center at 1 for
.
Notice that for
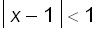
=
=
=
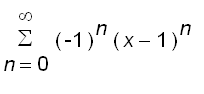
Therefore,
=
=
for
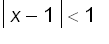
The radius of convergence of the required series is
.
The convergence for
:
Note that the interval of convergence of the series
is (
].
The convergence for
:
We can show, as in Example 5, that
for all
in (
].
Another way of doing this is to view
as a translation of
by
. In Example 5, we have shown that for all
in (
]
=
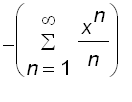
Thus, for all
such that
<
, that is for all
in (
],
=
=
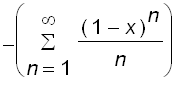
=
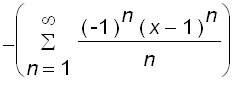
=
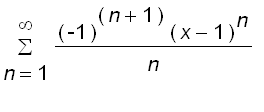
=
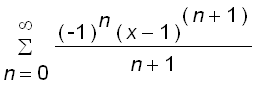
Example 9 Find a power series representation center at 2 for
and find the radius of convergence.
Since
, we can find the require series by integrating the power series center at 2 for
.
As in Example 8, we have
=
=
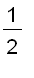
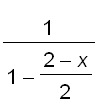
=
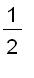
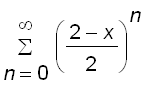
=
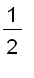
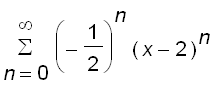
=
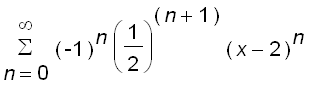
Notice that the above equations hold for
, that is,
.
Therefore, for
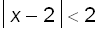
=
=
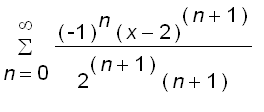
that is,
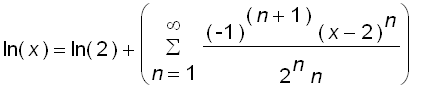
The radius of convergence of the required series is
.
![[Maple Plot]](images/suppl_powerSeriesRep252/suppl_powerSeriesRep252_001.jpg)
If
is a power series representation center at
for
, what do you think the radius of convergence of
should be ?
From the examples above, we have the following observations :
If function has a power series representation
, then
(1). For fixed
, the closer
is to
, the better
approximates
.
(2). For fixed
, the larger
is, the better
approximates
.
![[Maple Plot]](images/suppl_powerSeriesRep33/suppl_powerSeriesRep33_001.jpg)
![[Maple Plot]](images/suppl_powerSeriesRep206/suppl_powerSeriesRep206_001.jpg)
![[Maple Plot]](images/suppl_powerSeriesRep210/suppl_powerSeriesRep210_001.jpg)