¡@
Application of Integrals
Volumes by cylindrical Shells
![]()
Here we consider the problem of finding the volume of the solid
S
obtained by rotating about the
y
-axis the region bounded by
![]() =
=
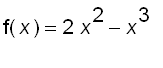 and
and
![]() .
.
![[Maple Plot]](images/suppl_solid_rev4.gif)
Here is an animation which shows how to generate the solid.
![[Maple Plot]](images/suppl_solid_rev5/suppl_solid_rev5_001.jpg)
It is difficult to handle this problem by the method introduced previously. Let's take another look of the solid.
![[Maple Plot]](images/suppl_solid_rev6/suppl_solid_rev6_001.jpg)
The animation above suggests that we may approximate the solid by cylindrical shells.
9 cylindrical shells :
![[Maple Plot]](images/suppl_solid_rev7.gif)
18 cylindrical shells :
![[Maple Plot]](images/suppl_solid_rev8.gif)
27 cylindrical shells :
![[Maple Plot]](images/suppl_solid_rev9.gif)
As we can see from the graphs above that total volume of the cylindrical shells gets closer and closer to the volume of the solid as the cylindrical shells get thinner and thinner.
![[Maple Plot]](images/suppl_solid_rev10.gif)
We divide the interval [![]() ] into n subintervals [
] into n subintervals [![]() ] of equal width
] of equal width
![]() and
let
and
let ![c[i] = (x[i-1]+x[i])/2](images/suppl_solid_rev14.gif) . If the rectangle with base [
. If the rectangle with base [![]() ] and height
] and height
![]() rotated about the
y
-axis, then the result is a cylindrical shell
rotated about the
y
-axis, then the result is a cylindrical shell
![]() with inner radius
with inner radius
![]() , outer radius
, outer radius
![]() and height
and height
![]() as illustrated above. The volume of
as illustrated above. The volume of
![]() is
is
![]() =
=
![]()
=
![]()
=
![]()
Therefore, an approximation to the volume of S is given by
![sum(V[i],i = 1 .. n) = sum(2*Pi*c[i]*f(c[i])*Delta*...](images/suppl_solid_rev26.gif)
This approximation become better as
![]() . From the definition of an integral, we get
. From the definition of an integral, we get
![limit(sum(2*Pi*c[i]*f(c[i])*Delta*x,i = 1 .. n),n =...](images/suppl_solid_rev28.gif)
Thus the volume of
S
is
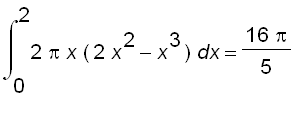 .
.
In the same manner, if
S
is the solid obtained by rotating about the y-axis the region bounded by
![]() ( where
( where
![]() ),
), ![]() ,
,
![]() , and
, and
![]() , then we can get that the volume of
S
is
, then we can get that the volume of
S
is
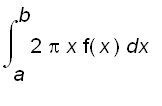
¡@
Let's conclude the methods of finding the volume of a solid of revolution with the following example.
To find the volume of the solid obtained by rotating about the
y
-axis the region between
![]() and
and
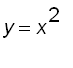 .
.
![[Maple Plot]](images/suppl_solid_rev38.gif)
Note that the intersection of the curves are (
![]() ) and (
) and (
![]() ).
).
A picture of the solid is shown below.
![[Maple Plot]](images/suppl_solid_rev41.gif)
![[Maple Plot]](images/suppl_solid_rev42.gif)
The region and a typical shell are shown above. We see that the shell has radius
![]() , and height
, and height
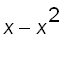 . So the volume is
. So the volume is
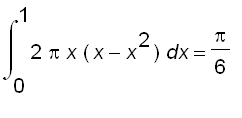
There is another way of looking at this.
![[Maple Plot]](images/suppl_solid_rev46.gif)
The cross-section perpendicular to
y
-axis at a distance of
y
from the origin is an annular ring with inner radius ![]() and outer radius
and outer radius
![]() , so the cross-sectional area is
, so the cross-sectional area is
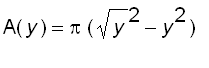
Therefore, the volume of the solid is
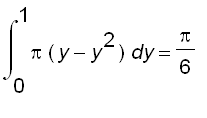
![]()