Application
of Integrals : Volumes
![]()
We all know that the volume of a right circular cylinder with radius
r
and height h
is 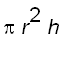 .
.
![[Maple Plot]](images/suppl_volume2.gif)
In general, a solid is called a cylinder (or right cylinder), as illustrated below, is bounded by a plane region B , called the base , and a congruent region B' in a parallel plane.
¡@
![[Maple Plot]](images/suppl_volume3.gif)
If the area of region B is A , then the cylinder has volume A h.
If we consider the cylinder with base { (
![]() ) |
) | 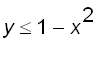 ,
, ![]() is in [
is in [![]() ] } and height h
as illustrated below :
] } and height h
as illustrated below :
![[Maple Plot]](images/suppl_volume8.gif)
We know that the area of the base is
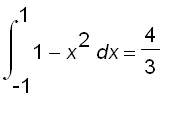 , so the volume of the solid is
, so the volume of the solid is 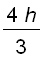 .
.
For a solid
S
that is not a cylinder we first "cut" S
into pieces and approximate each piece by a cylinder. For instance, let's consider the solid illustrated below, which is obtained rotating the region bounded by 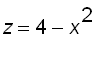 and
and ![]() about the z
-axis.
about the z
-axis.
![[Maple Plot]](images/suppl_volume13.gif)
We first "cut" the solid into n thin pieces. ( Click on the animation to see how it goes.)
![[Maple Plot]](images/suppl_volume14/suppl_volume14_001.jpg)
Since each horizontal cross-section ( the intersection of the solid and a plane) is a circle, we can approximate each piece by a circular cylinder.
n = 10 :
![[Maple Plot]](images/suppl_volume15.gif)
n = 20 :
![[Maple Plot]](images/suppl_volume16.gif)
Consider the piece cut by the horizontal plane with height
![]() and
and ![]() . From the graph above, we see that the radius r
of the cross-section at height z
is given by
. From the graph above, we see that the radius r
of the cross-section at height z
is given by ![r = sqrt(4-z[i])](images/suppl_volume19.gif) ( since
( since 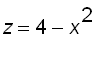 ).
).
![[Maple OLE 2.0 Object]](images/suppl_volume21.gif)
So we can approximate the piece by
![Pi*r^2*Delta*z = Pi*(4-z[i])*Delta*z](images/suppl_volume22.gif) . In this way, we get the total volume of all the pieces is given by
. In this way, we get the total volume of all the pieces is given by
![sum(Pi*(4-z[i])*Delta*z,i = 1 .. n)](images/suppl_volume23.gif)
The approximation become better and better as
![]() .( that is, the slices get thinner and thinner )
.( that is, the slices get thinner and thinner )
Therefore the volume of the solid is ![limit(sum(Pi*(4-z[i])*Delta*z,i = 1 .. n),n = infin...](images/suppl_volume25.gif) .
.
Let S be the solid that lies between
![]() and
and ![]() . If the cross-sectional area of S
in the plane
. If the cross-sectional area of S
in the plane ![]() , through
, through ![]() and perpendicular to the
x
-axis, is A(
x
), where A is a continuous function, then the volume of S
is
and perpendicular to the
x
-axis, is A(
x
), where A is a continuous function, then the volume of S
is
![limit(sum(A(x[i])*Delta*x,i = 1 .. n),n = infinity)...](images/suppl_volume30.gif)
Let's find the volume of a pyramid whose base is a square with side 2 and whose height is 2.
![[Maple Plot]](images/suppl_volume31.gif)
![[Maple Plot]](images/suppl_volume32/suppl_volume32_001.jpg)
As we can see from the graph above, each cross-section of the pyramid obtained by intersecting the plane
![]() (
(![]() )
)
is a square whose side a satisfies the equation
![a/2 = (2-z[i])/2](images/suppl_volume35.gif)
Hence the area of the cross-sectional area in
![]() is
is 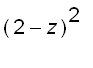 and the volume of the pyramid is
and the volume of the pyramid is
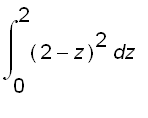 .
.
Can you find the volume of a pyramid whose base is a square with side a and whose height is h ?
A wedge is cut out of a circular cylinder of radius 4 by two planes. One plane is perpendicular to the axis of the cylinder. The other intersects the first at an angle of 30 degrees along a diameter of the cylinder. What is the volume of the wedge ?
![[Maple Plot]](images/suppl_volume39.gif)
![[Maple Plot]](images/suppl_volume40/suppl_volume40_001.jpg)
In the graphs above, we see that a cross-section perpendicular to the
x
-axis at distance x
from the origin is a triangle whose base is 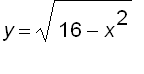 and whose height is
and whose height is 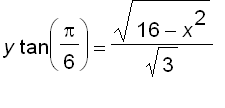 .
.
Thus, the cross-sectional area is 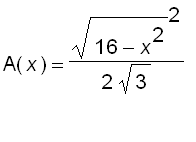 and the volume is
and the volume is
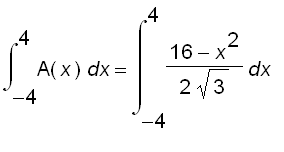 =
= 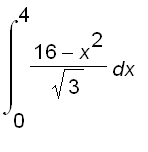 =
= 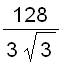 .
.
Now let's the solid obtained by rotation the region enclosed by the curves![]() and
and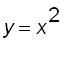 about the x
-axis. What is the volume of the solid ?
about the x
-axis. What is the volume of the solid ?
¡@
Here are animations of showing how we can get the solid :
1. The surface obtained by rotating the curve
![]() about the x
-axis.
about the x
-axis.
![[Maple Plot]](images/suppl_volume50/suppl_volume50_001.jpg)
2. The surface obtained by rotating the curve
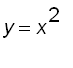 about the x
-axis.
about the x
-axis.
![[Maple Plot]](images/suppl_volume52/suppl_volume52_001.jpg)
3. Rotating the region enclosed by the curves
![]() and
and 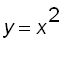 about the x
-axis.
about the x
-axis.
![[Maple Plot]](images/suppl_volume55/suppl_volume55_001.jpg)
Notice the the curves intersect each other at (
![]() ) and (
) and (
![]() ).
).
![[Maple Plot]](images/suppl_volume58.gif)
Here is a picture of the solid.
![[Maple Plot]](images/suppl_volume59.gif)
Here is an animation of the cross-section.
![[Maple Plot]](images/suppl_volume60/suppl_volume60_001.jpg)
In the animation above, we see that the cross-section in the plane
![]() is an annular ring with inner radius
is an annular ring with inner radius ![]() and outer radius
and outer radius ![]() , so the cross-sectional area is
, so the cross-sectional area is
![]()
Therefore, the volume of the solid is
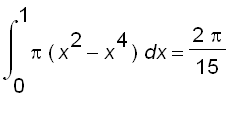 .
.
If the solid is obtained by rotation the region enclosed by the curves
![]() and
and 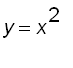 about
about ![]() . What is the volume of the solid ?
. What is the volume of the solid ?
Here is a picture of the solid.
![[Maple Plot]](images/suppl_volume69.gif)
![[Maple Plot]](images/suppl_volume70/suppl_volume70_001.jpg)
![[Maple Plot]](images/suppl_volume71/suppl_volume71_001.jpg)
In the animations above, we see that the cross-section in the plane
![]() is an annular ring with inner radius
is an annular ring with inner radius 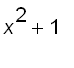 and outer radius
and outer radius ![]() , so the cross-sectional area is
, so the cross-sectional area is
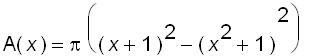
Therefore, the volume of the solid is
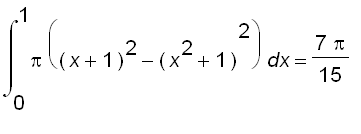 .
.