Back   Contents

{Gn} 是收斂的

令 ,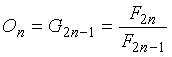  
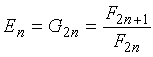
{O_n} 是 {G_n} 的奇數項所組成的數列：{G₁, G₃, G₅, ….. }
{E_n} 是 {G_n} 的偶數項所組成的數列：{G₂, G₄, G₆, ….. }

我們將證明：

1. {O_n}是遞增數列。

2. {E_n}是遞減數列。

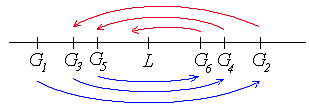
3. 對於所有的正整數 n，O_n < E_n；
   而且當 n 很大時，O_n 與 E_n 之間的距離會趨近於 0。

如下圖：

於是，由實數的稠密性可知：

{O_n} 與 {E_n} 一定會收斂到同一數 (暫且以 L 表示)。

換句話說，不論是 {G_2n-1 } 還是 {G_2n} 都會收斂到 L。

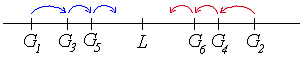
因此，{G_n} 也會收斂到 L。

證明：

0.     首先，我們要證明費氏數的一個神奇性質：F_{n + 2} F_n – F_{n + 1}² = (–1)^{n + 1}

利用數學歸納法：

a.      當 n = 1 時，
左式 = F₃ F₁ – F₂² = 2 – 1 = 1
右式 = (– 1)² = 1
故等式成立

b.     對任意自然數 n，若 n = k 時等式成立，即

F_{k + 2} F_k – F_{k + 1}² = (–1)^{k + 1}

當 n = k + 1 時，
左式 = F_{k + 3} F_{k + 1} – F_{k + 2}²
         = F_{k + 2} F_{k + 1} + F_{k + 1}² – F_{k + 2} F_{k + 1} – F_{k + 2} F_k
         = – (F_{k + 2} F_k – F_{k + 1}²)
         = (– 1) (–1)^{k + 1}
         = (–1)^{k + 2}
         = 右式
故等式成立

  由 a. b.及數學歸納法得證，F_{n + 2} F_n – F_{n + 1}² = (–1)^{n + 1}。
　

1. 證明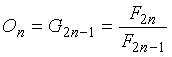：是遞增數列。

因為 分母 = F_{2n + 1} F_{2n – 1} > 0

         分子 = F_{2n + 2} F_{2n – 1} – F_2n F_{2n + 1}
                  = (F_{2n + 1} F_{2n – 1} – F_2n F_{2n – 1}) – (F_2n F_2n – F_2n F_{2n – 1})
                  = F_{2n + 1} F_{2n – 1} – F_2n²
                  = (– 1)²ⁿ            ß 利用先前證明的費氏數性質
                  = 1 > 0
　

2. 證明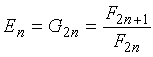： 是遞減數列。

因為 分母 = F_{2n + 2} F_2n > 0

         分子 = F_{2n + 3} F_2n – F_{2n + 1} F_{2n + 2}
                  = (F_{2n + 2} F_2n – F_{2n + 1} F_2n) – (F_{2n + 1} F_{2n + 1} – F_{2n + 1} F_2n)
                  = F_{2n + 2} F_2n – F_{2n + 1}²
                  = (– 1)^{2n + 1}            ß 利用先前證明的費氏數性質
                  = – 1 < 0
　

3. 證明：對於所有的正整數 n，O_n < E_n；
               而且當 n 很大時，O_n 與 E_n 之間的距離會趨近於 0。

因為 分母 = F_2n F_{2n – 1} > 0

         分子 = F_{2n + 1} F_{2n – 1} – F_2n F_2n = (– 1)²ⁿ = 1 > 0

另一方面，由於費氏數列是一個沒有上界的遞增數列，即
所以