玩久了「三、四、五」的型態,很容易便知道勝利的關鍵是什麼,玩起來也沒什麼意思。所以可以將銅板的列數或每一列的銅板數改變,這樣要找出所有規律就不太容易了。
直到本世紀初,哈佛大學數學系副教授查理士.理昂納德.包頓 (Charles Leonard Bouton) 才利用數的二進位表示法,解出了這個遊戲的一般法則:
對於任意列數,每列有任意枚數的銅板,致勝之道為何?包頓的方法很簡單。首先,將各列的銅板數化成二進位數,然後相加,但不進位。換句話說,就是
1 + 0 = 1
0 + 1 = 1
1 + 1 = 0
0 + 0 = 0再看一個例子:
1 + 1 + 1 = (1 + 1) + 1 = 0 + 1 = 1
於是我們知道:偶數個1相加會得到0,奇數個1相加會得到1。
如果遊戲規則為:最後將銅板拿光的人贏得遊戲。各列的銅板數化成二進位數相加之後(不進位)的每一位數都是0的狀況為安全殘局;相反地,只要其中有任何一位數是1,就是不安全殘局。
例如「三、四、五」遊戲,一開始就是不安全殘局,先拿的人可以適當取二枚(第一列取2枚)而造成安全殘局。

一般情形之下,將不安全殘局轉變成安全殘局的方法常常不只一種,如下:


為什麼安全殘局和不安全殘局可以利用上述的方法判定呢?這可以分成幾個部分來看:
若你留下上述所謂的安全殘局,即總和的每一位數都是0,由於不論對方取那一列的多少枚銅板,該列銅板數所對應的二進位數中,必定至少有一位數會由0變成1或者由1變成0,於是其總和的相對位數也會由0變成1。例如,{1,4,5}這個安全殘局,從第二列的4枚銅板中取走2枚,則
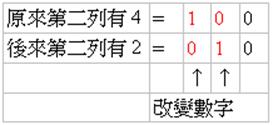

相反的,如果總和的某一位數是1,我們總有辦法在適當的列取走適當枚數的銅板,使得新總和的每一位數都是0。
首先,找出總和中所有是1的位數
其中
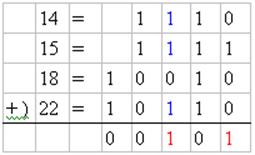
;在之前提到的例子{ 14, 15, 18, 22 }中,
={ 1, 3};也就是說,總和的第1位與第3位都是1。
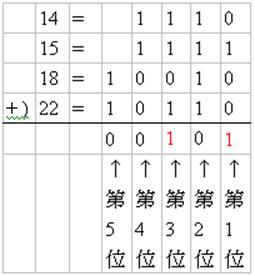
找出一列其銅板數之(二進位表示法)第
位數(也就是最左邊的一位,本例中是第3位)剛好是1;本例中,14(第一列)、15(第二列)、22(第三列)皆是。
接著改變該列二進位數中的所有
(
)位數值,亦即將0變為1,將1變為0。如此,我們會得到一個新數;以14(第一列)為例,14 = 1110,將其第1位與第3位改變,便得到1011 = 11枚銅板。
利用上面的方法,我們可以在該列中取走適當的銅板,使剩下的銅板數二進位總和的每一位數都是0;例如,在第一列取走14 – 11 = 3枚銅板。

反過來,若規定取走最後一枚銅板的人輸,也就是變成取完後的銅板數為0的人輸。之前的安全殘局現在變成了不安全殘局,而之前的不安全殘局也變成了安全殘局。所以若欲贏,就得讓取完後的二進位總和中至少有一位數是1。再來看看3, 4, 5的例子:






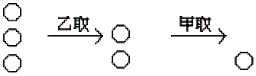 <甲勝>
<甲勝>
從以上的例子,你應該可以發現,前面幾步中,甲乙都可以留下自己的安全殘局,直到後來出現有某一列的銅板數大於1,而其他列都只剩一枚的情況。這時輪到甲來取,甲如何取就是勝負的關鍵:甲可以選擇將較多枚銅板的那一列拿光,或拿到只剩一枚。在這個例子中,甲選擇將該列拿到只剩一枚,因為這樣才能使剩下的列數為“奇數”,當然每一列均只有一枚銅板。顯而易見的是,以後一人取一列,到最後拿的一定是乙,於是甲必勝。
有很多人把這個方法寫成電腦程式,來和人對抗,不知就理的人被騙得團團轉,無不驚嘆電腦的神奇偉大。其實說穿了,只因為它計算比人快,數的轉化為二進位其速度快得非人能比,如此罷了。