Back   Contents

豆芽遊戲 (Sprouts)

尤拉公式

        若G為一連通之平面圖，則

V + F = E + 2

其中V代表G中點的個數，F代表G中面的個數，而E是G的邊數。

　

證明：

        我們可以用數學歸納法證明尤拉公式，在這裡要用兩層的數學歸納法：

1. 當F = 1時，

1. V = 1時成立。

V = 1, F = 1   E = 0   V + F = 1 + 1 = 0 + 2 = E + 2

2. 假設V = k – 1 時，尤拉公式成立，即

  (k – 1) + F = E + 2

對於一個包含k點及1個面的平面圖，即為一個有k點的樹，圖中沒有任何迴圈（否則有不只1個面）。因此，我們可以在這個圖上找到一個秩為1的點（樹的末端）使得拿掉這個點及與它相連的邊之後還是一個連通圖。

例如：

拿掉下圖中紅色的點及與它相連的邊，

仍然會是一個連通圖，如下面4種情況：

   

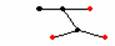
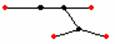
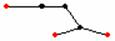
而拿掉一個秩為1的點後，就變成一個k – 1點的圖，由假設知

V + F = E + 2

當我們再把這個點放回去時，點數與邊數都會加1，所以

V' = V + 1,  E' = E + 1

則

V' + F = E'+ 2

（因為V + F = E + 2，當然 (V + 1) + F = (E + 1) + 2。）

由 1, 2 及數學歸納法得證，F = 1時尤拉公式成立。

2. 對任意自然數，假設 F = m – 1時尤拉公式成立。

對於一個有m（）個面的平面圖，圖中至少存在一個迴圈。我們可以在這迴圈中找一個位於兩個面交界的邊，使得拿掉這條邊後的面數少1，而圖形仍然連通。

例如：

拿掉下圖中的紅色邊，這個原本有3面的圖

就會剩下2面，如下面4種情況：

   

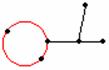
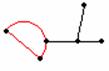
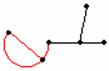
拿掉這條邊後，就變成一個m – 1面，由假設知

V + F = E + 2

當我們再把這個條邊放回去時，邊數與面數都會加1，所以

E' = E + 1,  F' = F + 1

則

V + F' = E' + 2

（因為V + F = E + 2，當然 V + (F + 1) = (E + 1) + 2。）

由 A, B 及數學歸納法得證V + F = E + 2。