1  2  3  4  5   Contents

豆芽遊戲 (Sprouts)

一定會結束嗎？

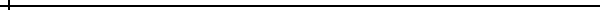
        了解遊戲規則後，也許有人會想：這個遊戲一定會結束嗎？會不會有一個可以一直加線的圖呢？別耽心，康威告訴你這個遊戲一定會在你加上第3n – 1條線時，或在那之前結束：

        遊戲規則告訴你，每個點都有三條“命”，也就是說，每個點都可以接出三條線。當一個點把它的三條命都用光，即接了三條線時，便“死”了，你再也不可以把其他線加到這個點上。因此，若遊戲開始時紙上有n個點，則紙上存在3n條命。然後你每加上一條線，就用掉兩條命（線有兩端，各用一條命），但你又在線上畫上一個新點，添了一條命。總體來看，就是每次都讓這個遊戲少一條命。

開始 3 + 3 + 3 = 9條命	第一步 3 + 2 + 2 + 1 = 8條命

當遊戲進行到最後剩下一條命時，就無法再加線，遊戲也就結束了。因此這個遊戲最多只能加上3n – 1條線。

　

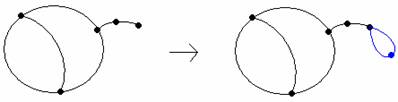
        如果遊戲結束時的圖為G₀，則圖裡所有點的秩，最小為2，最大為3。若是圖中有一點的秩為1，則遊戲仍可繼續，因為可以在該點上畫一個圈由自己連到自己，所以G₀中所有點的秩至少都是2；而秩最大為3是因為每個點只有3條命。

 

我們可以再將G₀變成圖G——其中所有點的秩都是3：

        假設x是一個秩為2的點，y是x的鄰居之一，於是我們拿走x，將原本與x相連的兩條邊接成一條，並將這條邊及y點塗成紅色，紀錄x的位置。

  

 

        連通的平面圖有一個特性：圖中的點數與面數之和恰等於邊數加2。這就是所謂的尤拉公式：

V + F = E + 2

其中V代表點的個數，F代表面的個數，而E是邊數。
　

讓我們看看幾個例子：

	V = 1, F = 1   E = 0   V + F = 1 + 1 = 0 + 2 = E + 2
	V = 2, F = 1   E = 1   V + F = 1 + 1 = 1 + 2 = E + 2
	V = 3, F = 2   E = 3   V + F = 3 + 2 = 3 + 2 = E + 2
	V = 5, F = 4   E = 7   V + F = 5 + 4 = 7 + 2 = E + 2

 

        有了這些資訊，我們便可以得到下面這個結論：

引理：

        假設遊戲開始時有m個點，遊戲玩了p次（加上3p條線）後結束，結束時的圖為G₀。若G (G₀)為一連通圖，則

f = 2 + p – m，

其中f是G₀的面數。 (證明)

 

        我們注意到，G中任一個面都一定只有一條紅色的邊，否則的話，表示在G₀中，這個面裡有兩個秩為2的點，如：

 

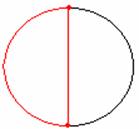
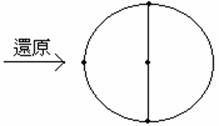
所以還可以加一條線連接這兩點，與遊戲已結束的假設矛盾。因此，紅邊的個數一定會小於或等於面的個數，若f為面的個數則 fr。若G不為一連通圖，我們可以將G分成若干連通部分(connected component)來討論，情形類似。因此我們只討論G為一連通圖之情形。

        若G為一連通圖，由引理我們知道 f = 2 + p – m，且 r = 3m – p，於是

2 + p – m  3m – p

得到

p  2m – 1

　

        遊戲是否可以在玩了2m – 1次（p =2m – 1）之後就結束呢？假設p = 2m – 1，由引理知：

f = 2 + p – m
  = 2 + (2m – 1) – m
  = m + 1

r = 3m – p
  = 3m – (2m – 1)
  = m + 1

得到 f = r，這表示每一個面都有一條紅邊，且不和其他面共用（否則f > r）。然而，因為G中每個點的秩皆為3，那麼G中至少存在一個迴圈 (Why?)。如果G中有迴圈，則看最小的迴圈，它會是一個封閉曲線，將平面分成圈內與圈外，如下圖中包圍黃面的迴圈：

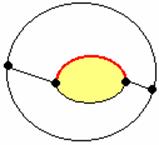
所以這個迴圈上的邊一定是兩個面的交界，也就是說，迴圈內的面一定得和其他面共用紅邊，與f = r矛盾。

        因此，一個開始時有m點的遊戲，至少要玩2m次才會結束，至多玩3m-1次就會結束。所以一個開始有3點的遊戲，至少要玩6次才可能結束，且最多只能玩9次就會結束。