Back   Contents

所有的偶完全數都是t_n = 2^n-1 × p這種型式，
其中p為麥爽質數 2ⁿ – 1。

<證明>

令a為一個偶完全數，則a = 2^n-1 × u, 其中 u為大於1的奇數，
因此 (a) = 2a = 2ⁿ × u。

又因為若m, n互質，則(mn) =(m)(n)。我們得知 

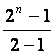
(a) = (2^n-1)(u) = (u)

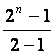
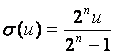所以 2ⁿ × u = (u)，而且  為整數。
 

因為2ⁿ 與2ⁿ – 1互質，所以 u必定是2ⁿ – 1的倍數。

假設，若  則 。然而

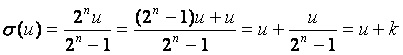
我們得到矛盾。
所以 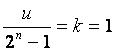，也就是  。

如此一來，我們得到 ；
也就是說u除了和夲身之外沒有其他因數，所以u是質數。

因此 a = 2^n-1 × u = 2^n-1 × (2ⁿ – 1)，而且2ⁿ – 1為質數。