1  2  3  4  5  6  7  8   Contents

完全數 (Perfect Number)

        我們讓s(n)表示其所有不為自身的因數的和；換句話說，s(n)(n) – n。

例如：

s(5) = (5) – 5 = 6 – 5 = 1
s(10) = (10) – 10 = 18 – 10 = 8
s(100) = (100) – 100 = 217 – 100 = 117
 

        對於一個自然數n，若s(n) = n（即(n) = 2n）我們便稱n為一個完全數。換句話說一個完全數為其所有不為自身的因數和。

例如： 

6 = 1 + 2 + 3
28 = 1 + 2 + 4 + 7 + 14

        這兩個數字對古代的猶太人與基督徒都意義重大，他們認為世界是在六日內被創造出來，而月亮環繞地球的週期則恰恰好是28日。雖然神可以在任何一瞬間創在出這個世界，但是祂卻選擇要用六日，因為六是完全數，意味天地萬物的完美。

        經過計算我們不難發現小於100的完全數只有6和28，那麼下一個完全數是什麼呢？我們可以利用數學軟體做計算，得到下一個完全數為496，大於496小於10000的完全數只有8128。

        我們注意到這四個數均為偶數而且都是2ⁿ × p，其中p為質數，的型式：

 6 = 2¹ × 3
28 = 2² × 7
496 = 2⁴ × 31
8128 = 2⁶ × 127

不只如此，其中的質數p都是麥爽質數（Mersenne prime）

6 = 2¹ × (2² – 1)
28 = 2² × (2³ – 1)
496 = 2⁴ × (2⁵ – 1)
8128 = 2⁶ × (2⁷ – 1)

 

        讓我們仔細看看2^k × p， p為質數，這一類的自然數：

若n = 2^k × p, 且p為質數，由上面(n)的計算公式（或直接算）：

 (n) = 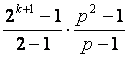= (2^k+1 – 1)(p + 1)

如果p是一個麥爽質數（Mersenne prime），也就是說，則

 (n) = (2^k+1 – 1)( 2^q) = 2^(k+1)+q – 2^q

若s(n) = n（即(n) = 2n），則

   2^(k+1)+q – 2^q
= 2 × (2^k × p)
= 2^k+1 × (2^q –1)
= 2^k+1+q – 2^k+1

因此，q = k + 1。

 

        若 n = 2^k–1 × p為完全數，其中p為麥爽質數，則

p = 2^k – 1。

反之，若p = 2^k– 1是質數，而n = 2^k–1 × p則  

(n) = (2 ^k – 1)(p + 1) = (2 ^k – 1) × 2^k = 2 × (2^k–1 × p) = 2 × n

因此， n = 2 ^k–1 × p = 2^k–1(2^k –1) 為一完全數。

 

        當然，這一類的完全數必定是偶數。是否所有的偶完全數都是這種型式？

尤拉（Euler）證明了所有的偶完全數都是這種型式。因此，偶完全數的問題又回到質數的問題，更清楚的說便是「那些n，可以使2ⁿ –1為質數？」。

黃色格子中的數字減1後便是麥爽質數，再乘上它前一個格子中的數就得到了完全數（2^n–1 × (2ⁿ –1)）。

　

是否存在奇完全數呢？

        雖然直至今日，數學家們已經確定在10³⁰⁰以內的數都沒有奇完全數，但是他們仍然相信：奇完全數沒有理由不存在。尤拉還證明了奇完全數一定是以下這種型式：m = p^4k+1Q²，其中p是一個4n +1型式的質數。其他數學家也先後證明了任何奇完全數都至少有6個不同的質因數；若這個奇完全數不是3的倍數，則至少會有11個不同的質因數；更進一步，要是這個奇完全數也不是5與7的倍數，則有至少26個不同的質因數。Stuyvaert並證明奇完全數一定是平方和的型式。