至於五色定理「任何平面地圖都能以五種顏色來著色」，我們可以用數學歸納法來證明：
我們這裡只須要考慮連通圖的情形，因為任意一個不連通圖都可以分成幾個小的連通圖，若這些小連通圖都能用五色來著色，則表示原本的不連通圖也可以用五種顏色來著色。
首先，一個只有一個點的圖一定沒問題。
假設所有n – 1（n
2）個點的平面圖都可以用5種顏色著色。那麼對於任何n個點的平面圖G，由性質4得知圖中一定有一個秩小於等於5的點x。將x自G中拿掉就可以得到一個n
– 1個點的圖，並由歸納法假設知道，這個新圖可以用5種顏色著色。
現在我們再把x放回去，若x的秩小於等於4的話，表示我們一定可以用一個顏色為x著色，而不會使得x和其他相鄰的點同色。
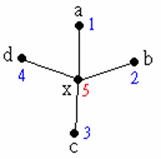
同樣地，如果x的秩等於5，但是有兩個或兩個以上的鄰居是塗同一種顏色，則我們還是可以輕易地為x上色。
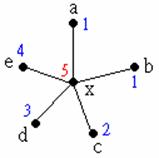
所以最後只剩下下圖這種情況，x有5個鄰居，每個鄰居的顏色都不一樣，這時x就沒辦法上色了。
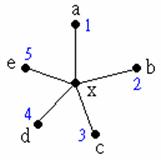
上圖中的英文字母表示點，數字表示顏色。
首先我們考慮自a出發的路徑中，所有由顏色為1的點與顏色為3的點交替形成的路徑—稱之為1-3路徑，並且假設沒有這樣的路徑連接a與c兩點。於是我們可以將這些路徑中的顏色1與3互換，使得a的顏色變成3。如下：
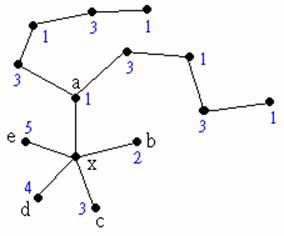
既然c不在這樣的路徑上，所以c的顏色仍然是3，於是我們現在可以放心地將x塗上顏色1，而不會使x與相鄰的五個點同色。
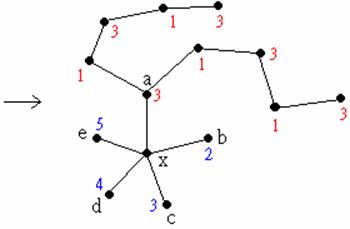
另一方面，若是a, c之間存在一條1-3路徑，那麼我們就考慮自b出發的路徑中，所有由顏色為2的點與顏色為4的點交替形成的路徑—亦即2-4路徑。我們發現a, c之間這條1-3路徑再加上(x, a)與(x, b)這兩條邊會形成一個迴圈，這使得b, d之間不可能有2-4路徑。
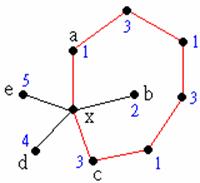
因此我們可以將所有自b出發的2-4路徑上的顏色2與4交換，b的顏色就變成了4，於是我們只要將x塗上顏色2，即完成這個五色圖。
由數學歸納法原理，我們證明了五色定理。
四色定理的證明和五色定理的證明有點類似，但複雜得多。阿倍爾和哈根探討平面圖的結構，建構了大約1500個「不可避免的形態」，使得任何一個平面地圖都可以變成點數較少的平面地圖。因為形態數目過多，在證明的過程中必須利用電腦來幫忙。