![]()
讓我們先討論一些平面連通圖的性質:
這裡我們討論的圖都是正規圖,所謂正規圖是指圖中任兩點間沒有重覆的邊,也沒有兩端連在同一點上的邊。也就是說下面的兩種情形
 或
或 
是不允許的。
平面圖 (planar graph):
一個圖如果可以畫在平面上使得所有的邊都互不跨越(端點除外),即為平面圖。雖然下圖中的紅邊橫跨藍邊,但是利用圖的同構性質,我們可以將紅邊拉出來,從外面走,便得到一個平面圖:
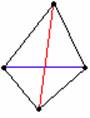
在圖論中,我們稱上面這兩個圖的關係為同構(isomorphism)。兩個同構的圖,它們點數相同,邊數相同,點與邊的關係也相同——如圖中的紅點,都以兩條黑線與另一紅點相連,並以一條綠線與綠點相連,而綠點則是分別以一條綠線與兩個紅點相連。
若G為一連通平面圖,則
v + f = e + 2
其中v代表G中點的個數,f 代表G中面的個數,而e是G的邊數。
(有關性質1及性質2請參閱「數學遊戲」單元中之「豆芽遊戲」部分。)
如果圖
G 是一個連通的平面圖,則圖中的邊數
(e) 一定小於等於點數
(v) 的3倍減6,即
e![]() 3v – 6。
3v – 6。
如果f > 1,也就是說圖中有至少兩個面,則每個面的邊界都有至少3個邊。否則就會產生下面的狀況:
或
這是正規圖中所不允許的。所以我們知道圖中至少有3f條邊界。
接著,以上圖為例,由於每一條邊都屬於一個或兩個面,但是對於紅色邊來說,在計算黃色區域的邊界時還是被算了兩次,因此
2e
3f
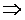
e
f = e – v + 2(尤拉公式:f + v = e + 2)
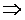
e
v – 2
e
3v – 6
任何正規的平面連通圖都有一個點的秩小於等於5。
如果我們可以找到一個每個點的秩都大於6的正規圖,則
2e = 所有秩的和 > 6v
3v < e
又 e
3v – 6,所以3v < e
3v – 6,產生矛盾。
所以任何正規圖都一定有一個秩小於等於5的點。