1  2  3  Contents

加法器的電路圖

        在討論加法器的電路圖之前讓我們先了解一下二進位的加法。以下是十進位與二進位的數字對照表：

十進位	二進位		十進位	二進位
0 1 2 3 4 5 6 7	000 001 010 011 100 101 110 111		08 09 10 11 12 13 14 15	1000 1001 1010 1011 1100 1101 1110 1111

二進位的四則運算與十進位的四則運算大同小異，唯一要注意的就是以二進位表示的數字，每位數都只能是0或1；就像以十進位表示的數，每位數只能是0, 1, 2,…, 8, 9其中的一個數。

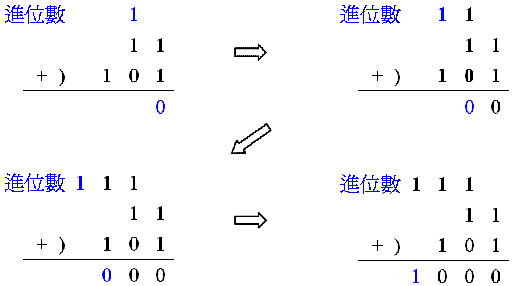
        二進位的加法中，若遇到1 + 1的情形，就該“進位”。以下是一個簡單的例子：11 + 101 = 1000 （3 + 5 = 8）

 
 

        假設P, Q為二進位的一位數（single binary digit），亦即0或1，那麼P + Q的可能情況有以下幾種：

1₂ + 1₂ = 0₂ = 10₂
1₂ + 0₂ = 1₂ = 01₂
0₂ + 1₂ = 1₂ = 01₂
0₂ + 0₂ = 0₂ = 00₂

所以這個電路的輸出值必需有二個位元，一個是用來儲存左邊的位元（稱為“進位數”(carry)），一個是用來儲存右邊的位元（稱為“和”(sum)）。“進位數”只有在P, Q都等於1的時候才會等於1，其他情況下皆為0。因此，我們可以在電路中放入一個“且”閘 ( PQ ) 來得到進位數。而當P, Q中一個是1另一個是0的時候，“和”就等於1。所以這可以用一個“EXOR”(PQ)(~( PQ)) 得到。於是，要計算兩個一位元的二進位數P, Q的電路圖可以以下圖表示。這種電路稱為“半加法器”(half-adder)。

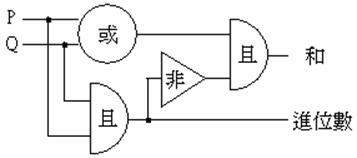
其真偽值表如下：

P	Q	進位數	和
1 1 0 0	1 0 1 0	1 0 0 0	0 1 1 0

　

        讓我們再想想如何設計一個電路去計算兩個二進位數的加法（亦即這兩個數不只有一位元）。在一般情形下，相加某一位元時很可能會產生一個進位數，於是在計算下一位元（左方的位元）的加法時，就變成要做三個一位元的數的加法——原本的兩個數的位元，以及之前的位元（右方的位元）相加所產生的進位數。如以下這個例子：

  

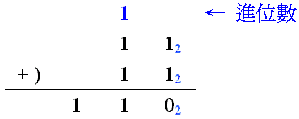
        所以若要設計一個夠做兩個多位元的二進位數加法的電路，就要讓它有能力計算三個一位元的二進位數加法。這樣的電路稱為“完全加法器”(full-adder)。現在讓我們考慮三個一位元的二進位數P, Q, R相加，輸出值仍然是“進位數”與“和”，分別以C, S表示。

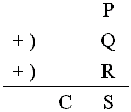
        完全加法器的運算中，每次也只取兩個數做相加，先將P, Q相加，其結果再與R相加，如以下的例子：

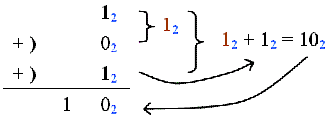
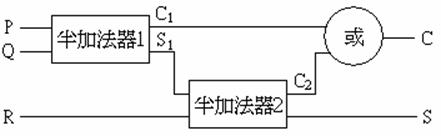
我們可以將完全加法器看成是半加法器的組合：

1.     利用半加法器將P, Q相加，得到二位元的數C₁S₁。

 

2.     再拿C₁S₁與R相加。

方法如下：

(a)   用半加法器做S₁與R的加法，得到二位元的數C₂S。此S即為總和的最右邊一位位元。

 

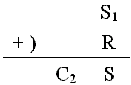
(b)   接著來算總和最左邊的一位位元C。首先，我們知道C₁, C₂不可能同時都是1——如果C₁是1，則P, Q都是1，因此 S₁是0，所以C₂不可能是1。既然C₁, C₂不可能同時為1，它們相加後就只會產生一個一位元的數C。而且，我們知道C只有當C₁或C₂是1的時候才會是1。 

P	Q	R	C	S
1 1 1 1 0 0 0 0	1 1 0 0 1 1 0 0	1 0 1 0 1 0 1 0	1 1 1 0 1 0 0 0	1 0 0 1 0 1 1 0

　

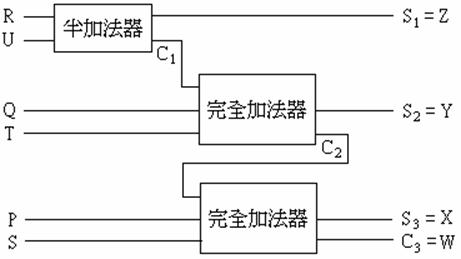
        兩個完全加法器與一個半加法器可以組合成一個功能更強大的加法器——平行加法器 (parallel adder)，它可以計算出兩個三位元數PQR, STU相加的結果，得到一個四位元數WXYZ，也就是 PQR + STU = WXYZ。當然，也可以利用類似的組合方法，使平行加法器可以計算任何（有限）位元數的加法。