|
現在我們要研究較複雜的雙變數(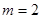 )純量函數( )純量函數(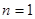 ),方程式如: ),方程式如: 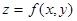 。一般會以對應的參數式 。一般會以對應的參數式
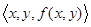 在 3 度空間作圖,稱為 2 維曲面(2D Surface)。或者以隱函數的方式呈現: 在 3 度空間作圖,稱為 2 維曲面(2D Surface)。或者以隱函數的方式呈現: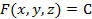 ,C 是常數, ,C 是常數,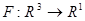 。 。
這裡的 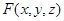 雖然本身是個 3 變數函數,但在條件限制其函數值必須保持一固定純量常數時,其中某個變數必將失去獨立性(independence),變成相依(dependent)於另二個變數;例如若是 z 相依於 x、y 這相依性以數學觀念呈現就是 雖然本身是個 3 變數函數,但在條件限制其函數值必須保持一固定純量常數時,其中某個變數必將失去獨立性(independence),變成相依(dependent)於另二個變數;例如若是 z 相依於 x、y 這相依性以數學觀念呈現就是 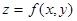 。意即以外觀是 3 變數的函數「隱」晦包藏著其實是
2 變數函數的本質(完整的隱函數探討是高等微積分的範疇)。 。意即以外觀是 3 變數的函數「隱」晦包藏著其實是
2 變數函數的本質(完整的隱函數探討是高等微積分的範疇)。
最簡單的例子:一次線性函數;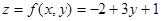 等價於 等價於 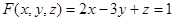 ,就是高中已經學過的「平面方程式」;若 ,就是高中已經學過的「平面方程式」;若 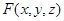 只是由 x、y、 z 的 2 次多項式所組成,則特稱為「二次曲面」(Quadric Surface),部分範例(橢圓、雙曲面、鞍面等)參見下面的
JAVA 習作。 只是由 x、y、 z 的 2 次多項式所組成,則特稱為「二次曲面」(Quadric Surface),部分範例(橢圓、雙曲面、鞍面等)參見下面的
JAVA 習作。
因為多變數函數的行為複雜,為了降低思考與做圖的困難常將部分變數先以常數值代入,例如 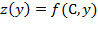 ,約化後是單變數
y 的函數,使問題能較容易處理。 ,約化後是單變數
y 的函數,使問題能較容易處理。
由幾何觀點解釋,就是以 x = C 平面去切截函數曲面
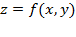 ,分析兩者的交集;也就是空間曲線 ,分析兩者的交集;也就是空間曲線 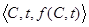 的變化行為(此處 的變化行為(此處
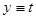 ),俾能進一步瞭解原來的多變數函數。 ),俾能進一步瞭解原來的多變數函數。
- 以下拉選單選取一個二次曲面。
- 再按扭選擇 x-y、y-z、x-z 任一種切截面
- 藉由Shift+、Shift-移動相交的位置
- 觀察切截曲線的類型與變化。
- 可調整透明度以得到最佳的空間透視
|