|
前面提到約化變數的手法,若對曲面方程式 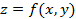 ,令 ,令
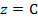 就得到一般稱之為「等高線」(level curve 或 contour)的隱函數方程 就得到一般稱之為「等高線」(level curve 或 contour)的隱函數方程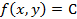 ,注意它本身是一條定義在
x-y 平面上的曲線(沒有
z 了);也可以想像這是以 ,注意它本身是一條定義在
x-y 平面上的曲線(沒有
z 了);也可以想像這是以
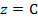 水平面去切截函數曲面所得交截線「投影」在x-y平面!可以從下面的
JAVA 範例清楚觀察到。等高線對於研究函數值的變化乃至連續性質、可微分性質以至極大極小值問題都是不可或缺的角色。在下面的範例中觀察曲面與其等高線的對應關係;等高線越密集處該區域的曲面是否坡度越陡峭? 水平面去切截函數曲面所得交截線「投影」在x-y平面!可以從下面的
JAVA 範例清楚觀察到。等高線對於研究函數值的變化乃至連續性質、可微分性質以至極大極小值問題都是不可或缺的角色。在下面的範例中觀察曲面與其等高線的對應關係;等高線越密集處該區域的曲面是否坡度越陡峭?
等高線
- 在下拉選單選取一個二次曲面。
- 藉由自動PLAY來移動截面相交的位置,觀察等高線變化。
- 可調整透明度以得到最佳的空間透視
|