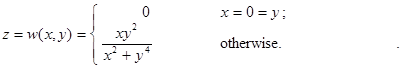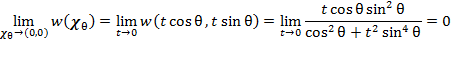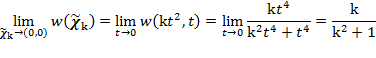EXAMPLE : 探討函數在原點的連續性質 II
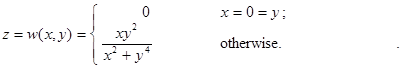
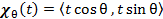 是通過原點並與x軸夾角 是通過原點並與x軸夾角 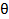 的路徑, 的路徑,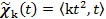 是沿著拋物線 是沿著拋物線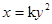 通過原點的路徑。 通過原點的路徑。
延續前一節對奇異函數曲面的處理手法;這一次
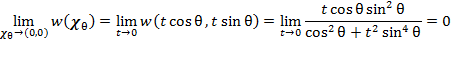
從任一角度的直線路徑逼近原點均得到同一極限值,但是我們仍不能驟下定論:「w 曲面在原點是連續的」!因為若沿 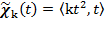 拋物線路徑逼近: 拋物線路徑逼近:
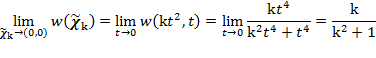
很明顯的,極限值將隨不同的 k 而完全不一致!結論是 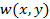 在 (0,0) 是不連續的。這個範例是否令你有所警惕? 在 (0,0) 是不連續的。這個範例是否令你有所警惕?
|
NOTE:光靠直線路徑約化函數的逼近極限仍不足以判斷函數本尊的極限與連續性!
|
比較以上四個奇異曲面的論證總結:
|
NOTE:在曲面的奇異點上,殊途同歸的各種路徑
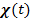 所對應的的空間曲線 所對應的的空間曲線 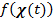 可不一定同「歸」。相異的逼近方式也許得到不同的極限! 可不一定同「歸」。相異的逼近方式也許得到不同的極限!
|
最後「極限與連續」其真正完備的意義是:
殊途同歸
函數在某處有極限值 if and only if 其任一路徑約化函數均在此處有同一極限值。函數在某處是連續的 if and only if 其任一路徑約化函數均在此處是連續的並有同一函數值。
接下來這個 JAVA 模組可以讓你自由定義三組不同類型的路徑,殊途同歸到原點,觀察個別空間曲線的行為,以及它們在整個函數曲面上的相對關聯性質。請將我們在此之前所有的代數分析過程做一次實地驗證,眼見為憑讓你更清楚體會這些方程式推導的真正用意。
- 在下拉選單選取一個奇異曲面。
- 在第二個下拉選單選取一種路徑模式,可以手動輸入起始點/終點的座標,亦可在第二視窗 x-y 定義域中以滑鼠左鍵點擊一處為起始點,滑鼠右鍵點擊處為終點(預設在原點)。
- 或者也可以選「自訂」模式,請以滑鼠左鍵拖曳出一條任意路徑
- 4. 按下預覽/開始/停止鍵
- 觀察不同的路徑對應奇異曲面上的空間曲線,極限值是否一致?
- 可調整透明度以得到最佳的空間透視
|