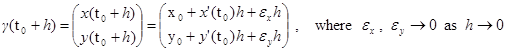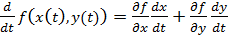向量函數

微分的證明與計算

在上一節的兩個對照範例中，我們看到：找出矛盾處，否證一函數的可微性比較容易，但若想由抽象的「可微分」定義以直接論證函數在某點可微，實際操作的難度較高。以下是一個我們較常用以判定可微性的間接證明工具：

THEOREM

If and exist and are continuous at point then is differentiable there.

NOTE：各偏導函數在某處都是連續的（如此想：各方向的切線的行為才會彼此有關連，意即共面），則函數在該點可微分！

至於多變數函數的「導函數」到底長啥樣子？必須要具備基本線性代數的知識才能再進一步描述；所謂的「線性映射」（linear mapping）或是「矩陣」（matrix）。

DID I GET THIS：可微分的驗證 II

多變數微分計算的技巧主要還是處理合成函數微分的Chain Rule公式，這裡以最簡單的基本型；單變數向量函數代入雙變數純量函數所合成的（其實就是路徑約化函數）來說明：

設因為在可微，所以

，代入 f 得到：

此處令，又因為在可微 , 所以上式進一步寫成：

, where as

,

, thus .

於是我們得到：

THEOREM

DID I GET THIS?

　