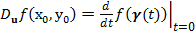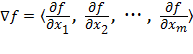|
現在我們已經知道函數 f 在點 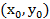 處,方向 處,方向 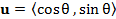 的方向導數: 的方向導數:
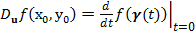 , where , where 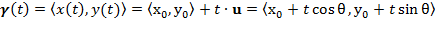
根據多變數 Chain
Rule:
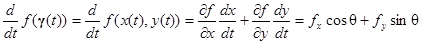
進一步寫成向量形式得到:
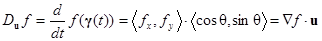
DEFINITION:多變數純量函數的 Gradient(梯度函數)
The Gradient
of 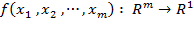 is the vector is the vector 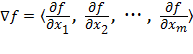
Gradient的一些重要意義:
以隱函數 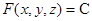 (C是純量常數)所定義的函數曲面(即 level surface 等位面,例如 (C是純量常數)所定義的函數曲面(即 level surface 等位面,例如 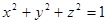 ),其上的 ),其上的 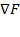 將處處垂直於此曲面;這是因為對曲面上的任一曲線路徑 將處處垂直於此曲面;這是因為對曲面上的任一曲線路徑 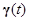 ,我們都有 ,我們都有 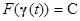 ,兩邊微分變成 ,兩邊微分變成 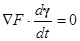 ,其中 ,其中 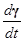 是曲線的(所以當然也是曲面的)切線向量,這意味 是曲線的(所以當然也是曲面的)切線向量,這意味 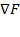 將與切平面上所有的切向量 將與切平面上所有的切向量
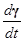 皆垂直,即 皆垂直,即 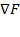 就是該切平面的法向量(Normal vector)!因此我們得到: 就是該切平面的法向量(Normal vector)!因此我們得到:
|
OBSERVATION:通過等位面上某一點
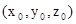 的切平面方程式是: 的切平面方程式是:
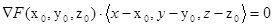
|
物理學中重力場的等位線(如衛星軌道)、電力場的等位面(如金屬導體表面)其Gradient就是重力、電磁力的方向(守恆力會垂直等位面)!下面的範例在最佳化理論(Optimization)中佔有一席之地(greedy algorithm的一種),所謂的「最陡峭路徑」(steepest
ascent/descent path),可以幫我們尋找某一起始點鄰近的極值位置:
- 在下拉選單選取一個曲面。
- 在右視窗觀察等高線與 Gradient 向量彼此互相垂直,又 Gradient 均指向函數值變大的方向。
- 在平面定義域(右視窗)中任意處以滑鼠左鍵點擊,就會自動顯示出該處的最陡路徑
- 可調整透明度以得到最佳的空間透視
|