1 2 3 4 5 6 7 8 9 10 11 12 Contents
早在十八世紀,大數學家尤拉就已經解決了七橋問題。非但如此,他同時注意到這個問題可以利用數學上的圖(graph在之前「數學遊戲」單元中我們介紹過,一個圖包含點及連接點的邊。)的語言理來描述,他以點代表城中被河水分隔的四個區域,並以邊代表連接各個區域的橋,如下圖:
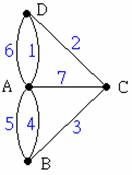
七橋問題就變成以下的問題:「是否存在一個迴圈通過每一條邊,而且每邊只經過一次?」這樣的迴圈我們稱之為尤拉迴圈。
因為圖中任兩點都有路徑相連,而且走的路徑起點和終點相同,因此我們從圖中任何一點出發結果都一樣。我們就從C點出發吧!
從C點我們可以選擇走向B點、A點或D點,由於B、D在圖上的相對位置是一樣的,所以從C往D走的情形和從C往B走的情形完全相同。
若C
D
A
從A我們不能走回D(死路!),因此走向C或B。然而C的秩為3,若自A走向C,則接下來就只能利用3走向B。這樣,就沒有路再回到C(終點和起點必須是同一點)!因此,A只能走向B;同上理,我們知道不能從B走向C,只能又再走回A。
若AB
A
D ,則無路可走;只能從A又再走回C,再從C出發後又同樣地沒有路回到C。
若C由走向A,由於B、D在圖上的相對位置是一樣的,所以從A往D走的情形和從A往B走的情形完全相同。我們就從走向B吧!
C
A
B
從B不能走向C,因為再從C出發後又同樣地沒有路回到C。只好走向A:
BA
D
A 卻又無路可走。
由 i, ii 我們發現無論怎麼走都無法得到一個通過每條邊各一次的迴圈。
各位注意到問題的徵結所在了嗎?----七橋問題之所以無解是因為上圖中存在奇數秩的點。
在做進一步的討論之前,我們需要介紹一些和圖有關的基本知識:
在一個圖中,點的秩(degree or valence)就是交會在這個點的邊的個數。如下圖中紅點的秩為3,藍點的秩為1。
![]()
我們說一個圖是一個連通圖,也就是說這個圖中的任兩點一定存在一個路徑相連。
當然,一個圖若有尤拉迴圈,這個圖一定是一個連通圖;而且如果沿著尤拉迴圈通過圖中除了起點之外的每個點時,一定是自圖中的某條邊連進去,並從另一條邊連出去。因此,除了起點之外的所有點,連進該點的邊數都等於連出該點的邊數,那麼每個點的秩都會是偶數。又因為迴圈最終還是要回到起點(中間可能進出多次),因此起點的秩也是偶數。
康尼斯堡的人尋找尤拉迴圈單純是好玩,然而這件事卻和管理科學中的最佳化問題有著密切的關連性(這其中包含要讓你的收益最大或支出最少的問題)。舉例來說,如何讓郵差、水電(或瓦斯)的抄表員或掃街車最有效率地完成工作?以郵差送信的問題來說,達成目的的方法是要設計一個路徑,讓郵差由所屬的郵局出發,走過需要經過的每一條街,而且盡量避免經過同一條街兩次,最後再回到郵局。
假設下圖是郵差所要送信的地區的街道圖,藍綠色部分為郵差應負責送信的區域,而其中橢圓形的區域為郵局所在:
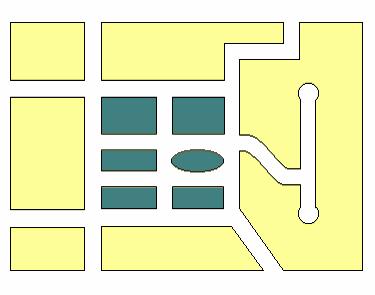
我們若用邊來代表每條街道,而用點來表示每個交叉路口,上圖可如下表示:

至於我們要做的兩件事:
要找一個通過每一條邊的路徑,而且每一條邊只能經過一次。
起點和終點必須相同。
這不就是要找尤拉迴圈(Eular circuit)的問題嗎?
熱身運動的過橋問題也是一個尋找尤拉迴圈的問題:
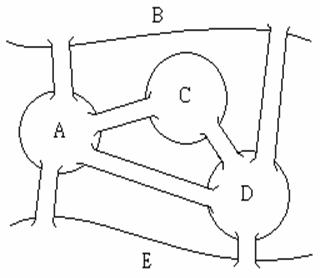
用點代表各個陸地區域,用邊代表每條橋,上面的地圖可以用下面的圖來表示:
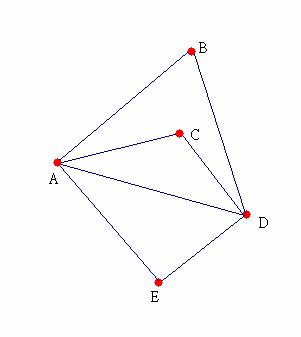
由之前的討論,我們知道如果圖中存在尤拉迴圈則此圖必為連通,並且圖中的每一個點都有偶數秩。對於任一個連通圖,如果圖中所有的點都有偶數秩,圖中是否一定存在尤拉迴圈?如果"是"的話,又如何將它找出來呢?