1 2 3 4 5 6 7 8 9 10 11 12 Contents
下面是一個連通圖,圖中每個點的秩都是偶數,我們是否可以在圖中找到尤拉迴圈呢?
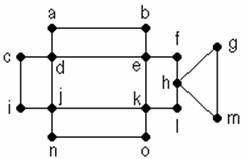
首先,我們自a點開始,任意畫一條封閉路徑,如
a-d-j-n-o-k-l-h-f-e-b-a。
由於每個點的秩都是偶數,也就是每個點都有偶數條邊與之相連,這使得當我們自a點出發,沿著路徑走至圖中的任何其他點,都不會是死路,在該點上一定還有其他邊讓你可以走出來,到下一點去,直到回到a點,而得到一個迴圈。若圖中有奇數秩的點,就不保證這件事情辦得到;因為一個奇數秩的點最終總會變成一個秩為1的點,於是當你走進這個點,就再也沒有路可以出來。
接下來,我們將紅色的迴圈拿掉不看,得到一個不連通的圖,但是圖中每個點的秩仍然是偶數。
這個圖可以分開看成兩個小連通圖,我們發現這兩個小圖都各有一個迴圈:
d-c-i-j-k-e-d與h-g-m-h。
將這兩個迴圈插入之前的迴圈:自a點開始,沿著紅色迴圈走,走至d點的時候,出來走綠色的迴圈,回到d點,繼續沿著紅色的迴圈走;走至h點時,再出來繞藍色迴圈,回到h點,繼續走完紅色迴圈回到a點。就得到這個尤拉迴圈
a-d-c-i-j-k-e-d-j-n-o-k-l-h-g-m-h-f-e-b-a
對於尤拉迴圈的存在性問題,十八世紀的數學家尤拉給了下面的解答:
「若一個連通圖中所有點的秩都是偶數,
則該圖中存在有尤拉迴圈;
反之亦然,若某圖中存在尤拉迴圈,
則該圖一定是一個由偶數秩的點所構成的連通圖。」假設圖G是一個連通圖,而且圖中每個點的秩都是偶數。那麼如同上面的例子,任意選一點a,由於圖中所有點的秩都是偶數,我們知道一定可以找到一個路徑,最終會回到a(途中也可能會經過a幾次)。將這個迴圈C自G中去掉,得到圖G’。就和之前的例子一樣,G’可能不再是連通圖,但是G’中的點的秩仍然是偶數。
我們知道C與G’一定會共用某幾個點,因為G可以分成C與G’兩部分,若C與G’之間不共點,則表示在G中C部分的點與G’部分的點間不存在有路徑相連,這與G是連通圖矛盾。那麼自C與G’共用的幾個點中任意選一點a’,然後自a’點出發,在G’中找一個迴圈C*。接著,在迴圈C的a’點插入迴圈C*,便得到一個大迴圈C’。
重覆同樣的動作,將C’自G中去掉,在剩下的圖中找一個迴圈C’’,再插入至C’中,得到更大的迴圈。以此類推,直到得到一個尤拉迴圈為止。