1  2  3  4  5  6  7  8  9  10  11  12   Contents

加權圖

        若將各個點間的距離也考慮進去，我們可以在每邊加上一個數字表示邊上的數字代表邊的長度，也就是點與點之間的距離，這樣的圖稱為「加權圖」。

例如：

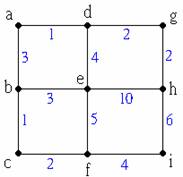
        圖中b, d, f, h都是奇數秩的點，利用這四點我們可以得到一個完全圖（即任兩點間都有邊相連），邊上的加權數就是該兩點在原圖中的最短路徑的長度。以b, d為例，由b至d的路徑有許多種走法，如b-a-d,  b-e-d,  b-e-h-g-d……等。

    

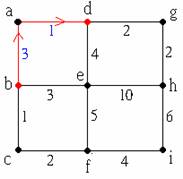
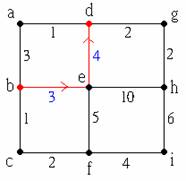
但是很顯然b-a-d是最短的一條路，只要走3 + 1 = 4個單位。

        同理，我們可以找出b, h間的最短路徑，長度為4個單位，如下；

以此類推，下面是b, f間、f, h間、d, f間以及b, h間的最短路徑，長度分別為3個單位、10個單位、7個單位及8個單位：

……

……

        因此我們可以得到下面的加一權完全圖：

接著在這個圖中將不相鄰的兩邊互相配對，如下圖的紅邊：

    

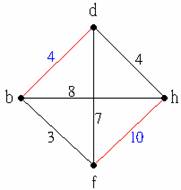
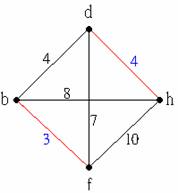
這些配對邊的加權和分別為14, 7, 15，既然希望路程愈短愈好，所以我們選擇{b, f}, {d, h}的這組邊。因此，我們要在原圖中加上兩條路徑分別連接b, f與d, h。而之前在畫完全圖計算邊上的加權時，就已經知道b-c-f是b, f間的最短路徑，而d-g-h是d, h間的最短路徑，所以我們可以順利地得到下面這個尤拉圖：

        這一類問題的應用其實不只在郵差送信，其他像清潔工掃街、瓦斯或水電的抄錶員也是同樣的問題，以色列的一家電力公司便是一個成功的案例。原來這家電力公司須要24名抄表員去負責某用户區域的抄表工作，管理單位的研究部門利用尤拉化的方法成功地尋找出有效率的抄表路線，將原夲所需的抄表時間縮短了百分之四十。之後，該區域只須要15名抄表員即可完成該區域的抄表工作。當然，有9名抄表員就沒飯吃了，不知道他們會不會詛咒尤拉？