1  2  3  4  5  Contents

單堆遊戲

雙倍遊戲的致勝法則解析：

        現在我們來解釋為什麼根據這樣的法則來玩必能致勝。

1. 如果n > 1，則< < 2。

<證明>

1. n = 2時，
   因為 = 2, = 3
   所以 < < 2

2. 假設對於所有的 n < k，< < 2成立
   因此我們有
              < < 2
              < < 2
   而費氏數又有以下性質：
              F_n = F_{n - 1} + F_{n – 2}
   故前兩式相加便得到
              < < 2

由 I, II 及數學歸納法得證。

 

2. 當火柴數n為費氏數時，後取者可勝。

[證明]

1. n = 2 =時，的確如此。

2. 假設當火柴數為比n小的費氏數時，後取者可勝。
   n為費氏數
   也就是 n =  （某一費氏數）
   而 =+ （>）

1. 甲若取根火柴
   由於 < 2
   乙便可全取根火柴
   甲輸

2. 甲為了避免(i)的情形，只好取少於根火柴。
   這時的情形可以考慮成一開始有根火柴，
   既然為比n小的費氏數，
   乙便可取適當火柴，而留下根火柴給甲。
   為比n小的費氏數，根據假設此情形對甲不利

由 I, II 及數學歸納法得證。

 

3. 當火柴數n不為費氏數時，先取者可勝。

[證明]

將 n 表示成不相鄰的費氏數之和：

n = ++ … +,
其中 …，且k₁k₂+2,  k₂k₃+2, … , k_r–1k_r+2

若甲取根火柴

由於 
              = +
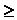
              > 2

所以乙只能取少於根火柴，

這時的情形可以考慮成一開始甲留根火柴給乙，

由 2 之討論得知，甲可取完此根中的最後一根火柴。

接著，因為之前甲取之火柴數必小於，

同樣的理由，乙只能取少於根火柴，

甲又可取完此根中乙未取完的部分。

以此類推，甲必可取到最後一堆根中的最後一根火柴。

 

我們以16根火柴為例，看看上面的策略如何執行：

16 = 13 + 3 ，

1613 乙只能取 1, 2, 3, 4，否則甲便能全取而勝

1312（12 = 8 + 3 + 1）1110 （10 = 8 + 2）

  8 7 （7 = 5 + 2）5….

6 （7 = 5 + 1）5….

 即如玩法四的分析中，討論 D 得知甲勝。

1311玩法四的分析中，討論 J 得知甲勝。

1310玩法四的分析中，討論 I 得知甲勝。

139玩法四的分析中，討論 H 得知甲勝。