1  2  3  4  5  6  7  8   Contents

埃及人的分數運算

        自古埃及保存至今的Rhind紙草紙(papyrus)上，記載著他們當時的算術技巧。首先看看埃及人如何計算41 × 59：

1. 先以加法得出下面的“倍乘表”：

 

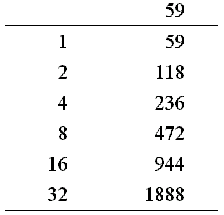
      （因為41 < 64，所以沒有必要再算64 × 59。）

2. 利用減法如下算出 41 = 32 + 8 + 1。

41 – 32 = 9,
9 – 8 = 1,
1 – 1 = 0.

這表示 41 × 59 = ( 32 + 8 + 1 ) × 59
= ( 32 × 59 ) + ( 8 × 59 ) + ( 1 × 59 )
= 1888 + 472 + 59
= 2419.

 

　

        古埃及人也許是藉著經驗得到這種算法，現在我們則知道可以利用整數的二進位表示得到 41 = 1 + 8 + 32：

41 = (1．2⁰) + (0．2¹) + (0．2²)+ (1．2³) + (0．2⁴) + (1．2⁵)
= (1．1) + (0．2) + (0．4)+ (1．8) + (0．16) + (1．32)
= (1．1) + (1．8) + (1．32)
= 1 + 8 + 32

  

        埃及人的除法是利用“平分表”來計算，例如1495 ÷ 65：

1. 計算65 + 65 = 130,  130 + 130 = 260, ……，直到算出一個數（此例中為1040），其兩倍會大於1495（2080 > 1495），但該數仍小於或等於1495。

2. 觀察右欄，我們知道1040 + 260 + 130 + 65 = 1495，對照左欄的數字，將它們加起來，得到 16 + 4 + 2 + 1 = 23，這表示：1495 ÷ 65 = 23。

 
 

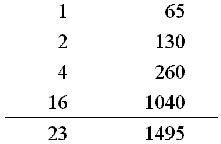
        當兩數不能整除的時候，埃及人也會用分數來表示。例如：53 ÷ 8

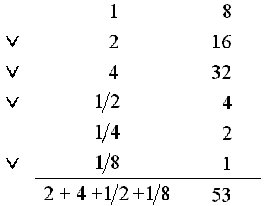
由於這樣的除法，埃及人的分數都以單位分數來表示。若遇到非單位分數，便將它轉換成幾個不同單位分數的和。例如 埃及人會記為 4 +。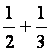
　

        為了運算的方便，埃及人製作了一個對照表以供查詢單位分數乘以2之後等於哪幾個單位分數的和。雖然我們都知道  = 2 ×  = +，但是埃及人卻偏偏寫成  = +。賴固德紙草書（Rhind papyrus）中發現了這樣的對照表：

至於以偶數為分母的單位分數，其兩倍後的結果很容易就可以看出來，例如：
 = 。

 

        埃及人如何利用上面的對照表來做分數運算？

例1： = + = ++

例2：求x，使得 ++ x = 1.

將等號兩邊的式子同乘15，就會將方程式轉換成10 + 1 + 15x = 15，於是

x =
= 2 × (2×)
= 2 × (+)
= +.

例3：(30 +) × (1 ++)

有了 (1 ++) 的二倍數、四倍數……之後，接著算 (1 ++) 的 ，因為

 × 1  = ,
 × =  = +,
 × =  = +,

所以 × (1 ++) = ++++

 既然 30 +  = 2 + 4 + 8 + 16 +

 

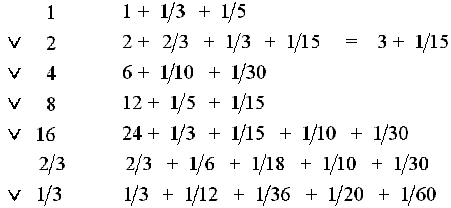
那麼

   (30 +) × (1 ++)
= (3 +) + (6 ++) + (12 ++)
   + (24 ++++) + (++++)
= 46 ++++++.

 

        如此複雜的分數計算自然阻礙了埃及人的算數及代數發展，然而卻引發一系列數論上的問題，諸如：

	是否每個有理數都可以用有限個不同的單位分數的和來表示？
	是否每個有理數都可以用7或更少個不同的單位分數的和來表示？
	是否每個有理數都可以用有限個不同的分母為奇數的單位分數的和來表示？