1  2  3  4  5  6  7  8   Contents

畢氏定理

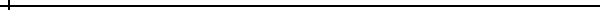
        若直角三角形的兩股長為a, b，斜邊長為c，則a² + b² = c²。人們相信這個定理是畢達哥拉斯〈約公元前560年~公元前480年〉發現的，因此把它叫做“畢氏定理”。而滿足a² + b² = c²的一組正整數解 a, b, c則稱為一組畢氏三元數（Pythagorean triples）。畢氏定理可以用簡單的幾何圖形來解釋：以直角三角形的三邊為邊長作出三個正方形，其中兩股上兩個正方形的面積和，會恰好等於斜邊上的正方形面積。

【http://sunsite.ubc.ca/LivingMathematics/V001N01/UBCExamples/Pythagoras/pythagoras.html】此網頁上有一個直觀的畢氏定理的幾何證明。

        早在公元前1100年，我們古代的數學家商高就已經知道“勾三股四弦五”，因此有人主張畢氏定理應為“商高定理”。商高是周朝的大夫，《周髀算經》（簡稱《周髀》）中記載了一段周公與商高之間的問答： 

周公問於商高曰：『竊聞乎大夫善數也，請問古者包犧立周天歷度。夫天不可階而升，地不可得尺寸而度，請問數安從出？』商高曰：『數之法出於圓方。圓出於方，方出於矩，矩出於九九八十一。故折矩，以為勾廣三、股修四、徑隅五。......此數之所生也……』

        但(3, 4, 5) 只是滿足畢氏定理的一組特殊解，一般性的定理一直等到陳子時代（公元前6, 7世紀）才出現，我們稱之為“勾股弦定理”或“勾股定理”，至於提出定理證明的則首推趙爽（公元3世紀）。趙爽，字君卿，三國時期吳國數學家，為《周髀算經》作注。在《周髀》卷上在周公、商高問答之後，有一個《弦圖》及趙君卿的注釋《勾股圓方圖說》。

   

 

        讓我們以現在的數學語言來解釋《勾股圓方圖說》：

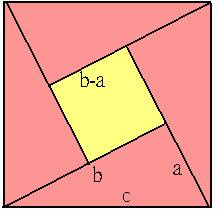
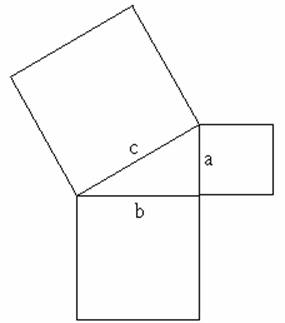
令a, b, c （b > a）為勾、股、弦之長度，以弦為邊作一正方形，其面積名為『弦實』，即。在那正方形內作四個直角三角形，塗以朱紅色，其面積名為『朱實』，即 ab/2。中央的小正方形，塗以黃色，其面積稱為『黃實』。而小正方形的邊長等於股、勾之差，即 ，因此黃實等於。但『弦實』等於四個『朱實』及『黃實』之和。也就是

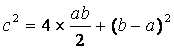
化簡則得

故得證『勾股各自乘并而開方除即弦』也就是 『弦² = 勾² + 股²』。十分巧妙吧？《弦圖》中所畫的情形雖然是邊長為3, 4, 5的三角形，但上面的證明卻是一般性的。

        歷史學家猜測西元前2000年左右，埃及人已經懂得使用畢氏三元數的關係來得到直角，這造就了他們在建築學上的非凡成就。他們先取12段等長的繩索接成一個圓環，接著固定一個接點，將圓環撐開，使其形成一個三角形，與固定點相連的兩邊分別是3段繩索與4段繩索，如下圖：

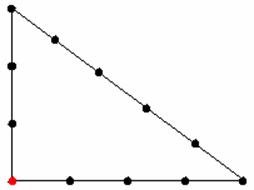
便得到一個邊長為3, 4, 5的直角三角形。

        這個方法利用了畢氏定理的反定理：

如果一個三角形的三邊滿足 c² = a² + b²,
則此三角形為一個以c為斜邊的直角三角形。

        另外，比畢達哥拉斯早一千年的巴比倫人，也已經會使用畢氏定理。在巴比倫，農人的財富是看他的莊稼產量，而莊稼的多寡又取決於此人擁有多少耕地面積。由這個角度看來，財富是用平方數（即正方形數）來計算：土地的面積即為該地長寬相乘之積，一塊長、寬都為a的土地，面積即為a的平方。

        巴比倫人感興趣的是，一個整數的平方是否可分割為其他數的平方和，以及什麼數可以如此被分割。若甲農夫有一塊25平方單位的土地，他便可以用它來交換兩塊土地，其中之一的面積為16平方單位，另一塊則是9平方單位，這表示一塊5 × 5的土地面積與一塊4 × 4和一塊3 × 3的土地面積總和相等。因此，5² = 3² + 4²對巴比倫人來說是一個實際問題的解答。

        在四十年代，考古學家紐格包爾 (O. Neugebeuer) 及沙爾斯（A. Sachs）發現了著名的普林頓322號泥板書（Plimpton 322，現存於哥倫比亞大學博物館）， 

據考證應存在於西元前1900至1600年左右，泥板上已經有15組畢氏三元數之計算。

        我們熟知的畢氏三元數有：(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17)等等，是否存在一個公式可以找出所有的畢氏三元數呢？畢氏學派除了證明畢氏定理之外，也證明了存在無限多組畢氏三元數。他們提出畢氏三元數的一組公式：

a = 2n + 1，b = 2n² + 2n，c = 2n² + 2n + 1

　

        我們已經知道「奇數和可以表示成一個正方形數」，如：

1 + 3 + 5 + 7 + 9 = 4²
1 + 3 + 5 + 7 + 9 = 5²

觀察一下，不難發現：

   4² + 9 = 5²,
即 4² + 3² = 5²

故 3, 4, 5 是一組畢氏三元數。

        又如：

1 + 3 + 5 + 7 + … + 23 + 25 = 12²
1 + 3 + 5 + 7 + … + 23 + 25 = 13²

於是有

   12² + 25 = 13²,
即 12² + 5² = 13²

故 5, 12, 13 也是一組畢氏三元數。

        觀察正方形數，我們知道n²個小石子組成的正方形再加上2n + 1個小石子就會構成一個更大的正方形—— (n + 1)²個小石子所組成的正方形，

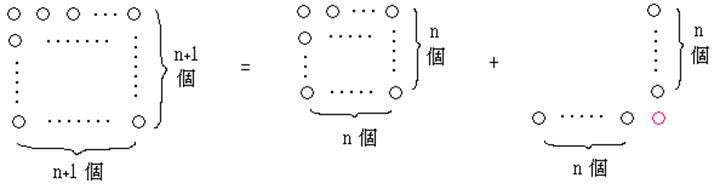
也就是說

n² + (2n + 1) = (n + 1)²

如果也是一個正方形數，即存在正整數m使得2n + 1 = m²，則

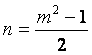
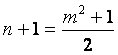
因此，

             

             

             

             

因此m, n, n+1也就是m, , 便構成了一組畢氏三元數。令m = 3, 5, 7, 9…，我們就可以依次得到3, 4, 5；5, 12, 13；7, 24, 25；9, 40, 41；…等無限多組畢氏三元數。這些畢氏三元數有一特徵：斜邊與直角的其中一邊相差1，如果將m表為2k + 1，則上述的畢氏三元數也可以表為2k + 1，2k² + 2k，2k² + 2k + 1。

        柏拉圖也給了另一組公式：

a = 2n，b = n² - 1，c = n² + 1

此時斜邊與其中一股之差為2。但他們都不是方程式a² + b² = c²的所有解，一般解的公式是

a = 2mn,  b = m² - n²,  c = m² + n²

其中m, n（m > n）為兩互質任意正整數。此公式的解法由丟番圖(Diophantus)約公元前250年首先提出。