1  2  3  4  5  6  7  8   Contents

怎樣尋找質數？

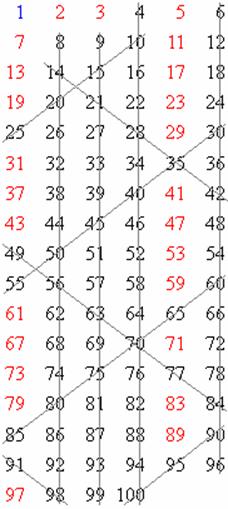
        我們要如何找出N以內的所有質數？

        首先，在紙上寫下1, 2, 3, … , N等N個數。接著，將除了2以外，所有是2的倍數的數劃掉；然後，2之後第一個沒有被劃掉的數是3，於是再劃掉除了3以外，所有是3的倍數的數；在3之後，第一個沒有被劃掉的數是5，所以要劃掉除了5之外，所有是5的倍數的數；以此類推，一直到為止（因為對於一個大於的數m而言，2m是2的倍數，3m是3的倍數，4m又是2的倍數，…，一直到 (m – 1)m是m – 1的倍數，它們早就被劃掉了，而m² > ()² = N，所以也不用考慮了）。於是，紙上還沒被劃掉的數，除了1之外，都是小於或等於N的質數。

        以N = 100為例，可以得到下表：

        也可以用類似的方法來檢驗一個整數N是否為質數：若所有小於或等於的質數都無法將N整除的話，N就是質數。但是當N很大的時候，要一一找出並檢驗所有小於或等於的質數是否可整除N就變得很繁複了，現在都將這種工作交給電腦來做。 

        質數在自然數中的分佈好像沒有什麼規則，為了研究質數的分佈情形，數學家用π(n)（這和圓周率沒什麼關係！）來表示小於n的質數個數。我們知道π(10) = 4，那麼π(100)呢？

        非但如此，由歐幾里得的定理，我們知道，隨著n的增加，π(n)值也不斷增大（意思是：若mn，則π(m)π(n)。）
 

        卡達迪（Cataldi）和費馬（Fermat）證明了：

「如果2ⁿ – 1是質數，則n必為質數。」

<證明>

假設n不是質數，則n可寫成兩個因數的乘積n = r × s
於是2ⁿ – 1就成了
2 ^rs – 1 = (2 ^r)^s – 1
= (2 ^r – 1)( (2 ^r)^s-1 + (2 ^r)^s-2 + … + 1)
因此2ⁿ – 1不是質數。
所以，若2ⁿ – 1是質數，n必定為質數。
　

        我們將2ⁿ – 1以M_n表示，稱為麥爽數（Mersenne number）。然而，若n是質數，M_n = 2ⁿ – 1並不一定就是質數。如：M₁₁ = 2¹¹ – 1 = 2047，可以被分解為23 × 89。目前，我們只找到三十多個是質數的麥爽數；儘管如此，人們還是相信是麥爽質數有無窮多個。

        早在二千多年前希臘人就發現M₂ = 3，M₃ = 7，M₅ = 31，和M₇ = 127是質數，這些n都還不大。但是n愈大時，要找新的麥爽質數就愈困難，因為後一個M_n’與前一個M_n差距愈來愈大，例如：第14個麥爽質數是M₆₀₇（183位數），第15個麥爽質數是M₁₂₇₉（386位數），它們相差多少倍已經不是可以用億或兆來衡量的了。
　

        1930年，美國數學家列默（D. H. Lehmer）把法國數學家魯卡斯（E. A. Lucas）在1876年發現來判別M_n是否為質數的快速檢驗法改進成了有名的：

「魯卡斯和列默檢驗法」

令s₁ = 4, s₂ = 4² – 2, s₃ = s– 2, … , s_{i + 1} = s– 2, …，

得出一序列 {s₁, s₂, s₃, s₄, …} = {4, 14, 194, 37634, …}

則對於p3，麥爽數M_p是質數的充分必要條件是s_{p - 1}能被M_p整除。
　

例如：M₃ = 7，s₂ = 14，而s₂ ÷ M₃ = 14 ÷ 7 = 2。
            M₅ = 31，s₄ = 37634，而s₄ ÷ M₅ = 37634 ÷ 31 = 1214。

       這個方法的好處是只用到乘法和加、減法的運算，而不須要一個一個找出所有小於或等於的質數，再一一檢驗是否會整除M_n。以後人們就用這個檢驗法並藉由電腦的協助找到了許多麥爽質數，如下表：

 

排序	n	位數	年份	發現者
1	2	1	古代
2	3	1	古代
3	5	2	古代
4	7	3	古代
5	13	4	1461	Reguis 1536, Cataldi 1603
6	17	6	1588	Cataldi 1603
7	19	6	1588	Cataldi 1603
8	31	10	1750	Euler 1772
9	61	19	1883	Pervouchine 1883, Seelhoff 1886
10	89	27	1911	Powers 1911
11	107	33	1913	Powers 1914
12	127	39	1876	Lucas 1876
13	521	157	1952	Lehmer 1952-3, Robinson 1952
14	607	183	1952	Lehmer 1952-3, Robinson 1952
15	1279	386	1952	Lehmer 1952-3, Robinson 1952
16	2203	664	1952	Lehmer 1952-3, Robinson 1952
17	2281	687	1952	Lehmer 1952-3, Robinson 1952
18	3217	969	1957	Riesel 1957
19	4253	1281	1961	Hurwitz 1961
20	4423	1332	1961	Hurwitz 1961
21	9689	2917	1963	Gillies 1964
22	9941	2993	1963	Gillies 1964
23	11213	3376	1963	Gillies 1964
24	19937	6002	1971	Tuckerman 1971
25	21701	6533	1978	Noll and Nickel 1980
26	23209	6987	1979	Noll 1980
27	44497	13395	1979	Nelson and Slowinski 1979
28	86243	25962	1982	Slowinski 1982
29	110503	33265	1988	Colquitt and Welsh 1991
30	132049	39751	1983	Slowinski 1988
31	216091	65050	1985	Slowinski 1989
32	756839	227832	1992	Gage and Slowinski 1992
33	859433	258716	1994	Gage and Slowinski 1994
34	1257787	378632	1996	Slowinski and Gage
35	1398269	420921	1996	Armengaud, Woltman, et al.
36	2976221	895832	1997	Spence, Woltman, GIMPS (Devlin 1997)
37	3021377	909526	1998	Clarkson, Woltman, Kurowski, GIMPS
38?	6972593	2098960	1999	Hajratwala, Woltman, Kurowski, GIMPS
39?	13466917	4053946	2001	Cameron, Woltman, GIMPS (Whitehouse 2001)

 

       以1979年發現的M₄₄₄₉₇為例，這個13395位數的新麥爽質數是由一位二十五歲的小伙子史洛汶斯基（D. Slowinski）發現，他使用一台每秒能做八千萬加法和乘法運算的電腦Cray找到這個數。四年後，他又用Cray電腦找到一個新的麥爽質數，共花費二百多小時的電腦計算時間，如此龐大的計算，就算是一個心算很好的數學家，恐怕得花上幾萬年才能得到這樣的結果。

       事實上，我們還不確定在M_3021377與M_6972593之間，及M_6972593與M_13466917之間是否還存在其他的麥爽質數，只能暫時稱M_6972593與M_13466917為第38個與第39個麥爽質數。

        近年來電腦運算的速度愈來愈快，更方便尋找最大的麥爽質數。欲知目前最大質數的情況，可由以下之網址查尋：http://www.utm.edu/research/primes/largest.html